Number of integral solutions to the equation where is equal to
To find the number of integral solutions to the equation x+y+z=21 under the constraints x≥1, y≥3, and z≥4, we can follow these steps:
Step 1: Change of Variables
We start by transforming the variables to eliminate the constraints:
- Let x=t+1 (since x≥1)
- Let y=m+3 (since y≥3)
- Let z=n+4 (since z≥4)
Step 2: Substitute into the Equation
Substituting these new variables into the original equation gives:
(t+1)+(m+3)+(n+4)=21
This simplifies to:
t+m+n+8=21
Step 3: Simplify the Equation
Now, we can simplify this equation:
t+m+n=21−8
t+m+n=13
Step 4: Count the Non-Negative Solutions
We need to find the number of non-negative integer solutions to the equation t+m+n=13. This can be solved using the "stars and bars" theorem, which states that the number of solutions to the equation x1+x2+…+xk=n in non-negative integers is given by:
(n+k−1k−1)
where n is the total sum we want (13 in this case) and k is the number of variables (3 here: t,m,n).
Step 5: Apply the Formula
In our case, n=13 and k=3:
Number of solutions=(13+3−13−1)=(152)
Step 6: Calculate the Binomial Coefficient
Now, we calculate (152):
(152)=15×142×1=2102=105
Conclusion
Thus, the number of integral solutions to the equation x+y+z=21 with the given constraints is 105.
We start by transforming the variables to eliminate the constraints:
- Let x=t+1 (since x≥1)
- Let y=m+3 (since y≥3)
- Let z=n+4 (since z≥4)
Substituting these new variables into the original equation gives:
(t+1)+(m+3)+(n+4)=21
This simplifies to:
t+m+n+8=21
Now, we can simplify this equation:
t+m+n=21−8
t+m+n=13
We need to find the number of non-negative integer solutions to the equation t+m+n=13. This can be solved using the "stars and bars" theorem, which states that the number of solutions to the equation x1+x2+…+xk=n in non-negative integers is given by:
(n+k−1k−1)
where n is the total sum we want (13 in this case) and k is the number of variables (3 here: t,m,n).
In our case, n=13 and k=3:
Number of solutions=(13+3−13−1)=(152)
Now, we calculate (152):
(152)=15×142×1=2102=105
Thus, the number of integral solutions to the equation x+y+z=21 with the given constraints is 105.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The number of integral solutions of the inequation x+y+z≤100,(x≥2,y≥3,z≥4) , is
A.100C2B.94C3C.93C2DNone of these - Question 2 - Select One
The number of integers solutions for the equation x+y+z+t=20, where x,y,z t are all ≥−1, is
A20C4B23C3C27C4D27C3 - Question 3 - Select One
The graphical solution of the system of linear inequalities 3x,4y≥12,y≥1,x≥0 is
A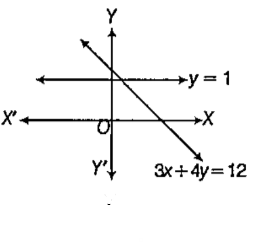 B
B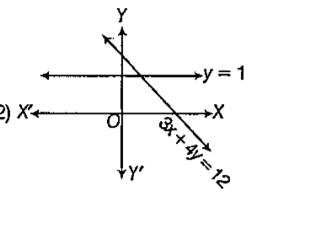 C
C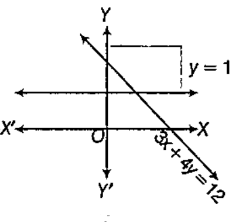 D
D