The rate constant for the first order deomposition of N2O5 is given by following equation:
logk=23.6−2×104KT
Calculate Ea for this reaction
[R=8.314JK−1mol−1]
To calculate the activation energy Ea for the first-order decomposition of N2O5 using the given equation for the rate constant k:
Step 1: Understand the given equation
The equation provided is:
logk=23.6−2×104T
This equation can be compared to the Arrhenius equation in logarithmic form:
logk=logA−Ea2.303RT
where:
- A is the pre-exponential factor,
- Ea is the activation energy,
- R is the gas constant (8.314 J K−1 mol−1),
- T is the temperature in Kelvin.
Step 2: Rearranging the equation
From the comparison of the two equations:
23.6=logA
and
−Ea2.303RT=−2×104T
From the second equation, we can equate:
Ea2.303RT=2×104T
Step 3: Isolate Ea
Multiply both sides by 2.303RT:
Ea=2×104×2.303R
Step 4: Substitute the value of R
Now, substitute the value of R:
Ea=2×104×2.303×8.314
Step 5: Calculate Ea
Now, calculate the value:
Ea=2×104×2.303×8.314
Calculating this step-by-step:
1. Calculate 2.303×8.314:
2.303×8.314≈19.189
2. Now multiply by 2×104:
Ea≈2×104×19.189≈383,780 J/mol
3. Convert to kJ/mol:
Ea≈383.78 kJ/mol
Final Answer
The activation energy Ea for the reaction is approximately:
Ea≈383.78 kJ/mol
---
The equation provided is:
logk=23.6−2×104T
This equation can be compared to the Arrhenius equation in logarithmic form:
logk=logA−Ea2.303RT
where:
- A is the pre-exponential factor,
- Ea is the activation energy,
- R is the gas constant (8.314 J K−1 mol−1),
- T is the temperature in Kelvin.
From the comparison of the two equations:
23.6=logA
and
−Ea2.303RT=−2×104T
From the second equation, we can equate:
Ea2.303RT=2×104T
Multiply both sides by 2.303RT:
Ea=2×104×2.303R
Now, substitute the value of R:
Ea=2×104×2.303×8.314
Now, calculate the value:
Ea=2×104×2.303×8.314
Calculating this step-by-step:
1. Calculate 2.303×8.314:
2.303×8.314≈19.189
2. Now multiply by 2×104:
Ea≈2×104×19.189≈383,780 J/mol
3. Convert to kJ/mol:
Ea≈383.78 kJ/mol
The activation energy Ea for the reaction is approximately:
Ea≈383.78 kJ/mol
Topper's Solved these Questions
Similar Questions
The rate constant for the first order decomposition of H2O2 is given by the following equation : log K = 14.2 - 1.0×104TK
Calculate Ea for this reaction and rate constant k if its half life period be 200 minutes. (Given : R = 8.314 JK−1mol−1)
View SolutionThe rate constant for the first order decomposition of N2O5 is given by the following equation: k=(2.5×1014s−1)e(−25000K)/T
Calculate Ea for this reaction and rate constant if its half-life period be 300 minutes.
View Solution
Knowledge Check
The rate constant for a first order reaction becomes six times when the temperature is raised from 350 K to 400 K. Calculate the activation energy for the reaction
[R=8.314JK−1mol−1]A4.17kJmol−1B41.7kJmol−1C417.0kJmol−1D4170kJmol−1The rate constant of a first orrder reaction becomes six times when the temperature is raised from 350 K to 400 K. Calculate the activation energy of the reaction (R=8.314 JK−1 mol−1)
A4.17 kJ mol−1B41.7 kJ mol−1C417.0 kJ mol−1D417.0 kJ mol−1The rate constant for the first order decomposition of ethylene oxide into CH4 and CO,
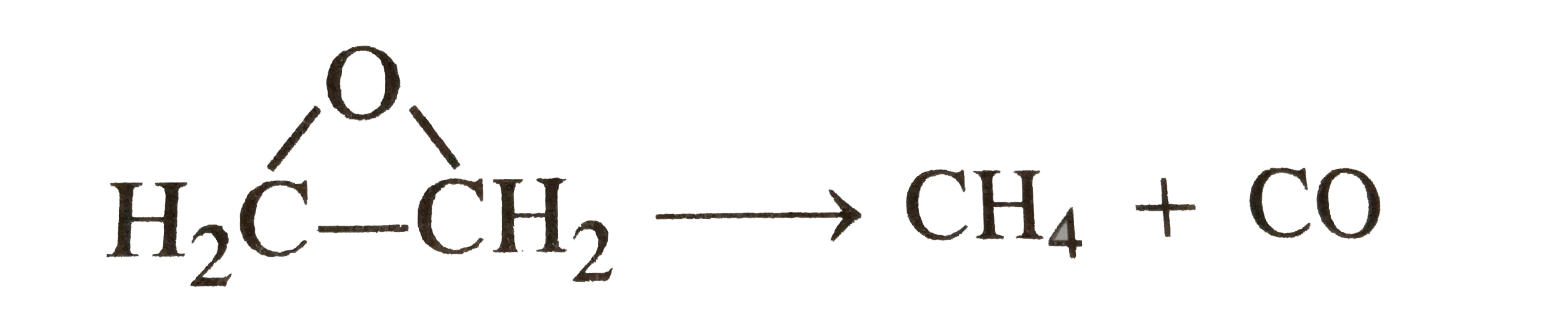
may be describe by
logk(ins−1)=14.34−1.25×104KT
The activation energy of the reaction isA4.8×10−5kJmol−1B4.8×105kJmol−1C2.39×102kJmol−1D2.39×105kJmol−1
The rate constant for the first order decomposition of H2O2 is given by the following equation :
logk=14.2−1.0×104T
Calculate Ea for this reaction and rate constant k if its half-life period be 200 minutes.
[Given : R=8.314JK−1mol−1]
View SolutionThe rate constant for a first order decomposition reaction is given by log K=10 - 1000/T .Then,what will be activation energy in kcal/mol?
View SolutionThe rate constant for a first order decomposition reaction is given by "log K=10−1000T .Then,what will be activation energy in kcal/mol?
View SolutionThe rate constant of a reaction is 1.5×107s−1 at 50∘C and 4.5×107s−1 at 100∘C. Calculate the value of activation energy for the reaction (R=8.314JK−1mol−1)
View SolutionThe first order rate constant for the decomposition of N2O5 is 6.2×10−4s−1. The t1/2 of decomposition is
View Solution
