Area of a quadrant of a circle of radius 7cm is
154cm2
77cm2
772cm2
774cm2
To find the area of a quadrant of a circle with a radius of 7 cm, we can follow these steps:
1. Understand the Formula for Area of a Quadrant:
The area of a quadrant of a circle is given by the formula:
Area of Quadrant=14πr2
where r is the radius of the circle.
2. Substitute the Radius:
Given that the radius r=7 cm, we substitute this value into the formula:
Area=14π(7)2
3. Calculate r2:
Calculate 72:
72=49
So, the formula now becomes:
Area=14π(49)
4. Substitute the Value of π:
We can use π≈227 for our calculations:
Area=14×227×49
5. Simplify the Expression:
Now, we can simplify the expression:
Area=14×22×497
First, calculate 22×49:
22×49=1078
Now, substitute this back:
Area=14×10787
6. Calculate the Area:
Now, we can simplify further:
Area=10784×7=107828
Now, divide 1078 by 28:
1078÷28=38.5
7. Final Result:
Thus, the area of the quadrant is:
Area=38.5cm2
The area of a quadrant of a circle is given by the formula:
Area of Quadrant=14πr2
where r is the radius of the circle.
Given that the radius r=7 cm, we substitute this value into the formula:
Area=14π(7)2
Calculate 72:
72=49
So, the formula now becomes:
Area=14π(49)
We can use π≈227 for our calculations:
Area=14×227×49
Now, we can simplify the expression:
Area=14×22×497
First, calculate 22×49:
22×49=1078
Now, substitute this back:
Area=14×10787
Now, we can simplify further:
Area=10784×7=107828
Now, divide 1078 by 28:
1078÷28=38.5
Thus, the area of the quadrant is:
Area=38.5cm2
Topper's Solved these Questions
Similar Questions
From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in Fig. 12.23. Find the area of the remaining portion of the square.
View Solution.A quadrant of a circle of radius 7 cm is rolled into a cone. Find the slant height and height of the cone
View Solution
Knowledge Check
The perimeter of a quadrant of a circle of radius 'r' is :
Aπr2B2πrCr2[π+4]D2πr+r2The perimeter of a quadrant of a circle of radius 'r' is :
A≠r2B2πrCr2[π+4]D2πr+r2In the given figure, ABCD is a rectangle inscribed in a quadrant of a circle of radius 10 cm. If AD=√25 cm then area of the rectangle is
 A32cm2B40cm2C44cm2D48cm2
A32cm2B40cm2C44cm2D48cm2
BCP is a quadrant of a circle of radius 14cm. With AC as diameter, a semi-circle is drawn. Find the area of the shaded portion.
View SolutionABCP is a quadrant of a circle of radius 14 cm. With AC as diameter, a semi-circle is drawn. Find the area of the shaded portion.
View SolutionIn the given figure, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.
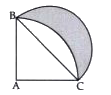
View SolutionABCP is a quadrant of a circle of radius 14 cm. with AC as diameter, a semicircle is drawn. Find the area of the shaded portion
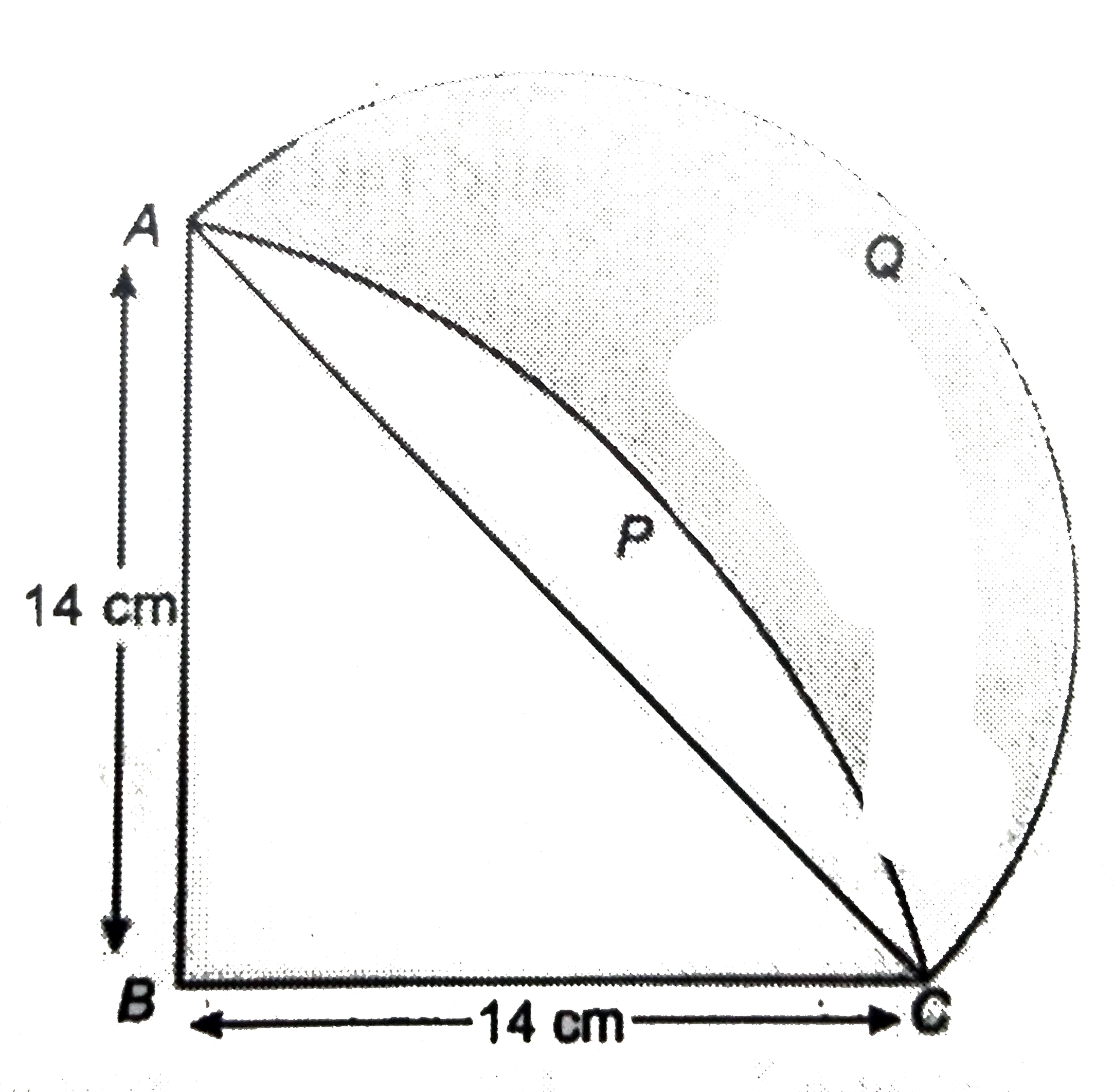
View SolutionFind the perimeter of the quadrant of a circle of radius 14 cm.
View Solution
