State Of Gas|Types Of Processes|Internal Energy|Work Done By Gas|Polyt

A process in which work perfomed by an ideal gas is proportional to the corresponding increment of its internal energy is described as a polytropic process. If we represent work done by a ppolytropic process by $W$ and increase in internal energy as $Δ U$ then
$W \propto Δ U$
or $W = K_{1} Δ U$ ...(i)
For this process, it can be demonstrated that the relation between pressure and volume is given by the equation
$P V^{η} = K_{2}$ (constant ) .....(ii)
We know that a gas can have various values for molar specific heats. The molar specific heat $' C'$ for an ideal gas in polytropic process can be calculated with the help of first law of thermodynamics. In polytropic process process the variation of molar specific heat $' C'$ with $η$ for a monatomic gas is plotted as in the graph shown.
ocr_image
In the graph shown, the $y -$ coordinate of point $A$ is ( for monatomic gas )

View Solution

A process in which work perfomed by an ideal gas is proportional to the corresponding increment of its internal energy is described as a polytropic process. If we represent work done by a ppolytropic process by $W$ and increase in internal energy as $Δ U$ then
$W \propto Δ U$
or $W = K_{1} Δ U$ ...(i)
For this process, it can be demonstrated that the relation between pressure and volume is given by the equation
$P V^{η} = K_{2}$ (constant ) .....(ii)
We know that a gas can have various values for molar specific heats. The molar specific heat $' C'$ for an ideal gas in polytropic process can be calculated with the help of first law of thermodynamics. In polytropic process process the variation of molar specific heat $' C'$ with $η$ for a monatomic gas is plotted as in the graph shown.
ocr_image
In the graph shown, the $y -$ coordinate of point $A$ is ( for monatomic gas )

View Solution

For an ideal gas,
(i) the change in internal energy in a constant pressure process from temperature $T_{1}$ to $T_{2}$ is equal to $n C_{V} (T_{2} - T_{1})$ , where $C_{V}$ is the molar heat capacity at constant volume and $n$ is the number of moles of the gas
(ii) The change in internal enregy of the gas and the work done by the gas are equal in magnitude in an adiabatic process.
(iii) The internal energy does not change in an isothermal process. ltbr> (iv) no heat is added or removed in an adiabatic process

View Solution

Assertion: In a thermodynamic process, initial volume of gas is equal to final volume of gas. Work done by gas in this process should be zero
Reason: Work done by gas in isochoric process is zero.

View Solution

Find the work done by the gas in the process $A B C$ .
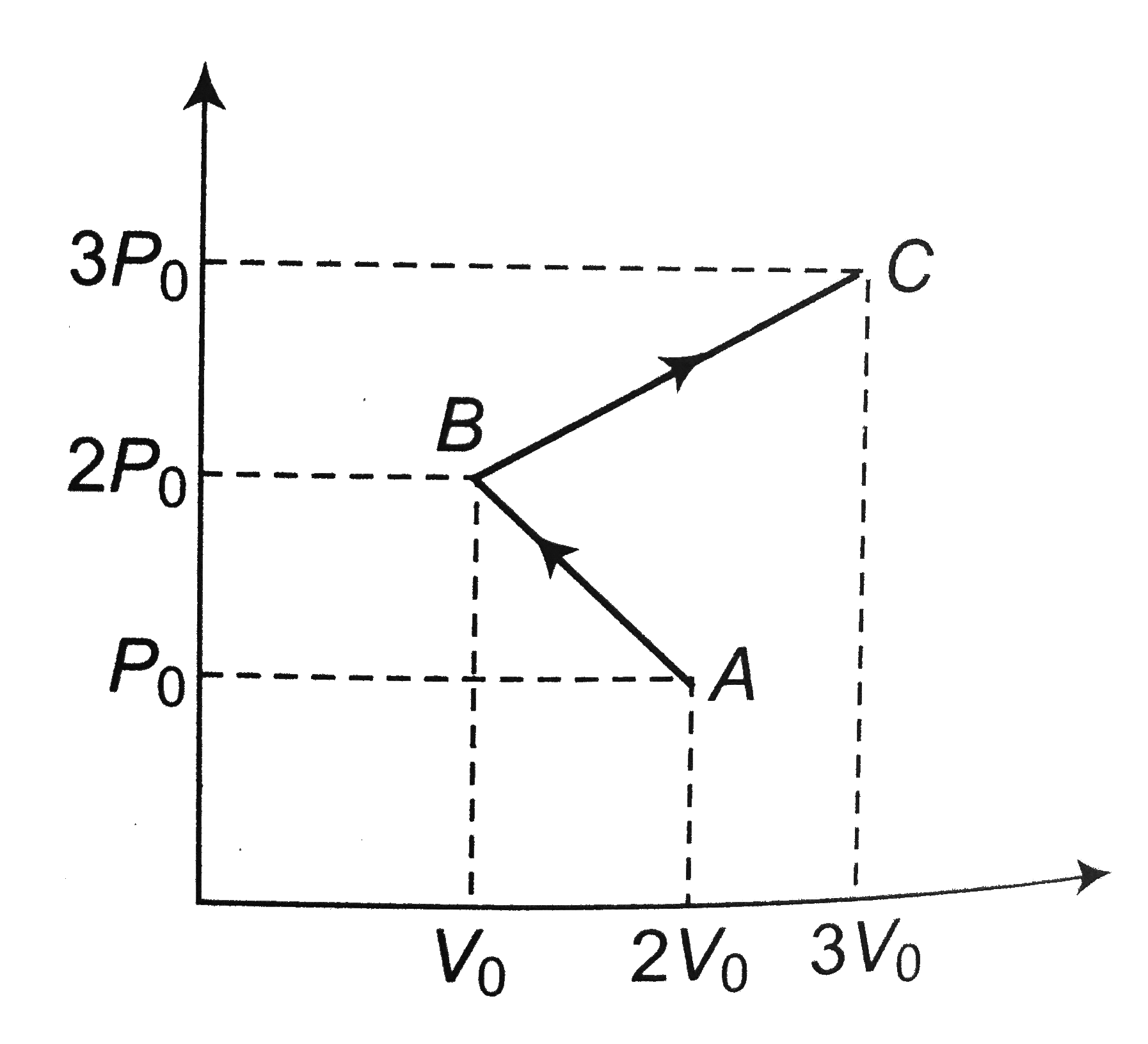
ocr_image

View Solution

State Of Gas|Types Of Processes|Internal Energy|Work Done By Gas|Polytropic Process

Similar Questions

Knowledge Check

In a cyclic process, the internal energy of the gas

In a cyclic process, the internal energy of the gas

Recommended Questions