A metal block of mass m is suspended from a rigid support through a metal wire of diameter 14 mm.The tensile stress developed in the wire under equilibrium state is 7×105 Nm−2.The value of mass m is _____ kg.(Take,g=9.8 ms−2and π=22/7)
To solve the problem, we need to find the mass m of the metal block suspended from a wire. We will use the relationship between tensile stress, mass, gravitational acceleration, and the dimensions of the wire.
1. Understand the formula for tensile stress:
The tensile stress σ in a wire is given by the formula:
σ=FA
where F is the force applied (which is equal to the weight of the block, mg), and A is the cross-sectional area of the wire.
2. Calculate the cross-sectional area A:
The cross-sectional area A of the wire can be calculated using the formula for the area of a circle:
A=πr2
where r is the radius of the wire. Given the diameter d=14mm, we can find the radius:
r=d2=14mm2=7mm=7×10−3m
Now, substituting r into the area formula:
A=π(7×10−3)2=π×49×10−6m2
Using π≈227:
A=227×49×10−6=10787×10−6≈154×10−6m2
3. Relate tensile stress to mass:
From the definition of tensile stress:
σ=mgA
Rearranging this gives:
m=σAg
4. Substituting the values:
We know:
- σ=7×105N/m2
- A≈154×10−6m2
- g=9.8m/s2
Now substituting these values into the equation for m:
m=(7×105)×(154×10−6)9.8
5. Calculating the mass m:
First calculate the numerator:
7×105×154×10−6=1078×10−1=107.8
Now divide by g:
m=107.89.8≈11kg
Final Answer:
The value of mass m is 11kg.
The tensile stress σ in a wire is given by the formula:
σ=FA
where F is the force applied (which is equal to the weight of the block, mg), and A is the cross-sectional area of the wire.
The cross-sectional area A of the wire can be calculated using the formula for the area of a circle:
A=πr2
where r is the radius of the wire. Given the diameter d=14mm, we can find the radius:
r=d2=14mm2=7mm=7×10−3m
Now, substituting r into the area formula:
A=π(7×10−3)2=π×49×10−6m2
Using π≈227:
A=227×49×10−6=10787×10−6≈154×10−6m2
From the definition of tensile stress:
σ=mgA
Rearranging this gives:
m=σAg
We know:
- σ=7×105N/m2
- A≈154×10−6m2
- g=9.8m/s2
m=(7×105)×(154×10−6)9.8
First calculate the numerator:
7×105×154×10−6=1078×10−1=107.8
Now divide by g:
m=107.89.8≈11kg
The value of mass m is 11kg.
Topper's Solved these Questions
Similar Questions
A load of 4.0 kg is suspended from a ceiling through a steel wire of radius 2.0 mm. find the tensile stress developed in the wire when equilibrium is achieved. Take g=3.1πms−2
View SolutionA transverse wave of speed 70 m/s is set up in an aluminum wire of diameter 1.60 mm. Calculate the tension in wire if its density is 2.7×103kg/m3.
View Solution
Knowledge Check
A metal wire of length L is suspended vertically from a rigid support. When a bob of mass M is attached to the lower end of wire, the elongation of the wire is l:
AThe loss in gravitational potential energy of mass M is Mgl.BThe elastic potential energy stored in the wire is MglCThe elastic potential energy stored in the wire is 12MglDHeat produced is loss of mechanical energy of system is 12MglA load of 4kg is suspended from a ceiling through a steel wire of length 20m and radius 2mm. It is found that the length of the wire increases by 0.031mm, as equilibrium is achieved. If g=3.1×πms(−2), the value of young's modulus of the material of the wire (in Nm−2) is
A(A) 2×1012B(B) 4×1011C(C) 2×1011D(D) 0.02×109Two blocks of masses 2.9 kg and 1.9 kg are suspended from a rigid support S by two inextensible wires each of length 1 m. The upper wire has negligible mass and the lower wire has a uniform mass of 0.2 kg/m. Thewhole system of block, wire and support have an upward acceleration of 0.2 m/s2. g = 9.8 m/s2. The tension at the mid-point of lower wire is-
 A10NB20NC30ND50N
A10NB20NC30ND50N
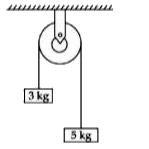
Two blocks of masses 3 kg and 5 kg are connected by a metal wire going over a smooth pulley. The breaking stress of the metal is 24π×102Nm−2 . What is the minimum radius of the wire ?
(take g=10ms−2)
View SolutionThe speed of transverse waves produced in a copper wire is 40 m/s. Calculate the tension developed in the wire if diameter of wire is 1.8 mm and density of wire is 8.9×103kgm−3.
View SolutionTwo blocks of mass 2.9 kg and 1.9 kg are suspended from a rigid support S by two inextensible wires each of length 1 meter, see fig. The upper wire has negligible mass and the lower wire has a uniform mass of 0.2kg/m. The whole system of blocks wires and support have an upward acceleration of 0.2m/s2. Acceleration due to gravity is 9.8m/s2.
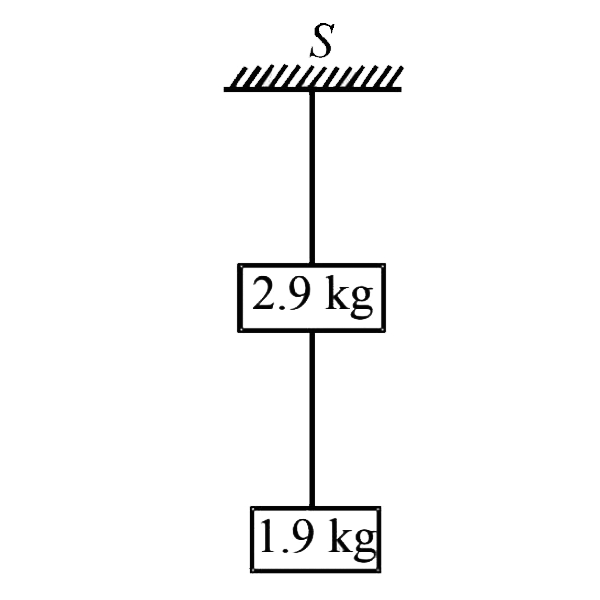
(i) Find the tension at the mid-point of the lower wire.
(ii) Find the tension at the mid-point of the upper wire.
View SolutionA load of 4 kg is suspended from a ceiling through a steel wire of length 2 m and radius 2 mm. It is found that the length of the wire increase by 0.032 mm as equilibrium is achieved. What would be the Young's modulus of steel ? (Take , g=3.1πms−2)
View SolutionA load of 4.0 kg is suspended from a celling through a streel wire of length 2.0 m and radius 2.0 mm. It is found that the length of the wire increases by 0.031 mm as equilibrium is achieved. Taking g=3.1πms−2 the Young's modulus of steel is
View Solution
