A hydraulic automobile lift is designed to lift vehicles of mass 5000 kg. The area of cross section of the cylinder carrying the load is 250cm2.The maximum pressure the smaller piston would have to bear is___
[Assume g = 10ms2 ]:
200×10+6 Pa
20×10+6 Pa
2×10+6 Pa
2×10+5 Pa
To solve the problem of finding the maximum pressure the smaller piston would have to bear in a hydraulic lift designed to lift vehicles of mass 5000 kg, we can follow these steps:
1. Identify the Given Values:
- Mass of the vehicle, m=5000kg
- Acceleration due to gravity, g=10m/s2
- Area of cross-section of the cylinder, A=250cm2
2. Convert Area from cm² to m²:
- Since 1cm2=10−4m2,
A=250cm2=250×10−4m2=0.025m2
3. Calculate the Force Exerted by the Vehicle:
- The force F exerted by the vehicle due to gravity is given by:
F=m⋅g=5000kg×10m/s2=50000N
4. Calculate the Pressure:
- Pressure P is defined as force per unit area:
P=FA=50000N0.025m2
- Performing the calculation:
P=500000.025=2000000N/m2
5. Express Pressure in Pascal:
- Since 1N/m2=1Pa, we can express the pressure as:
P=2×106Pa
6. Final Result:
- The maximum pressure the smaller piston would have to bear is:
2×106Pa
- Mass of the vehicle, m=5000kg
- Acceleration due to gravity, g=10m/s2
- Area of cross-section of the cylinder, A=250cm2
- Since 1cm2=10−4m2,
A=250cm2=250×10−4m2=0.025m2
- The force F exerted by the vehicle due to gravity is given by:
F=m⋅g=5000kg×10m/s2=50000N
- Pressure P is defined as force per unit area:
P=FA=50000N0.025m2
- Performing the calculation:
P=500000.025=2000000N/m2
- Since 1N/m2=1Pa, we can express the pressure as:
P=2×106Pa
- The maximum pressure the smaller piston would have to bear is:
2×106Pa
Topper's Solved these Questions
Similar Questions
A hydraulic automobile lift is designed to lift cars with a maximum mass of 3000Kg. The area of cross section of the piston carrying the load is 425cm2. What maximum pressures would the smaller piston have to bear?
View SolutionA hydraulic automobile lift is designed to lift cars with a maximum mass of 300 kg. the area of cross-section of the piston carrying the load is 425cm3. What maximum pressure would smaller piston have to bear?
View Solution
Knowledge Check
A crane lifts a mass of 100 kg to a height of 10 m in 20 s. The power of the crane is (Take g=10ms−2)
A100 WB200 WC250 WD500 WThe diameter of the piston of a hydraulic automobile is D metre. What pressure, in atmosphere is required to lift a car of mass m kg ?
A4mgπD2×105B2mgπD2CmgπD2D105×4mgπD2The mass of lift is 500 kg. When it ascends with an acceleration of 2m/s2,the tension in the cable will be [g=10m/s2]
A6000 NB5000 NC4000 ND50 N
A car of mass 1400 kg placed on the platform in a service station has to be lifted up. The area of the press piston to which the platform is 5m2. Determine the force that has to be applied on the piston of pump cylinder having an area of cross section 0⋅25m2.
(Take g = 10 m s−2)
View SolutionA lift is designed to carry a load of 4000 kg through 10 floors of a building, avarage 6m per floor, in 10s. Calculate the power of the lift.
View SolutionA crane lifts a mass of 100 kg to a height of 10 min. 20 sec. The power of the crane is (Take g =10m/s2)
View SolutionA crane lifts a mass of 100kg to a height of 10m in 20s. The power of the crane is (Takeg=10ms−2)
View SolutionA lift of mass 1000 kg is going up. The variation in the speed of lift is shown in figure. Then the minimum tension in the rope will be (g=10m/s2)
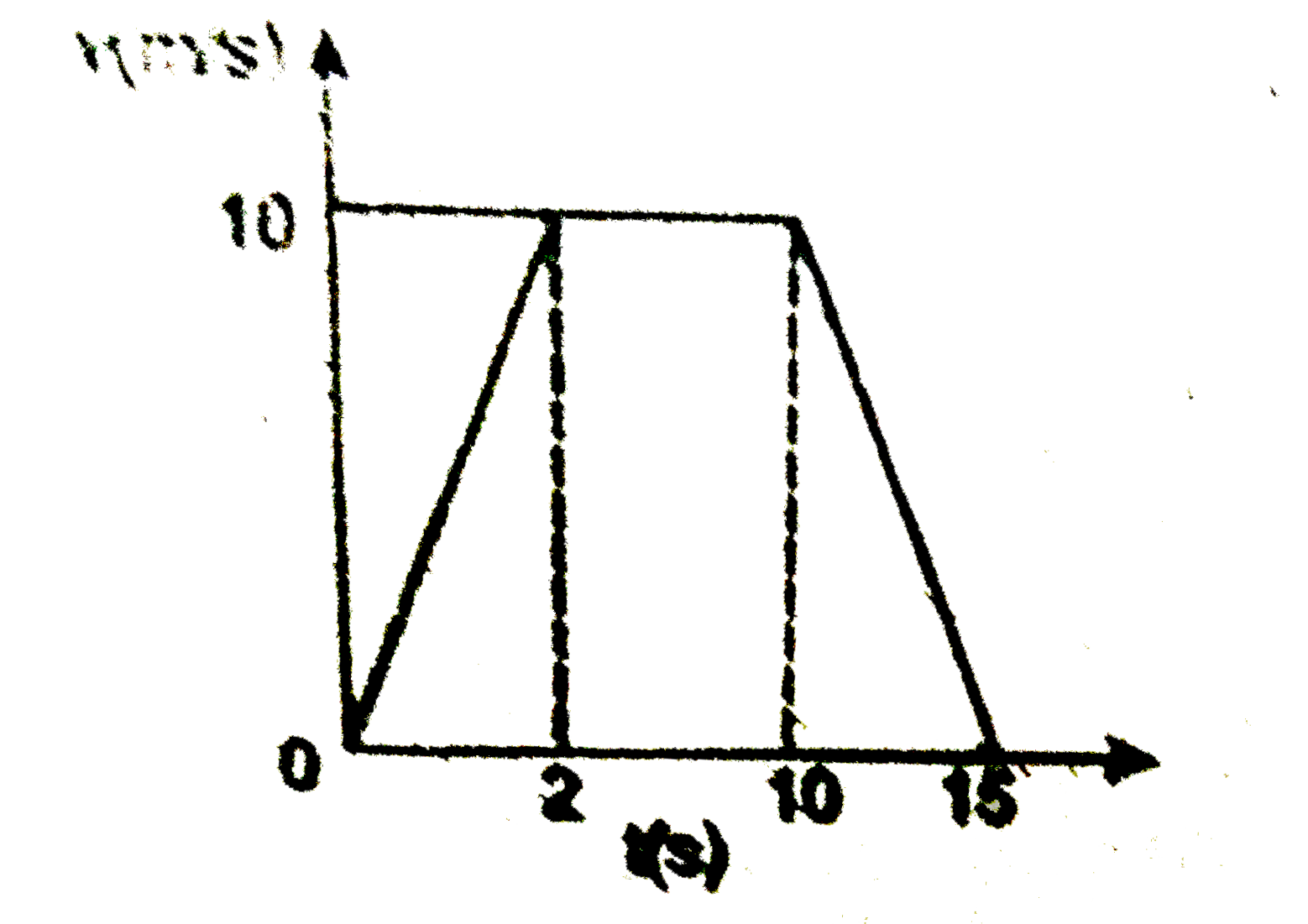
View Solution
