Two radioactive elements A and B initially have same number of atoms.The half life of A is same as the average life of B. If λ_Aandlambda_B are decay constants of A and B respectively,then choose the correct relation from the given options:
λ_Aln2=λB
λ_A=2λB
λ_A=λB
λ_A=λBln_2
To solve the problem, we need to establish the relationship between the decay constants of two radioactive elements A and B, given that their half-lives and average lives are related.
1. Understanding Half-Life and Average Life:
- The half-life t1/2 of a radioactive element is given by the formula:
t1/2=ln2λ
where λ is the decay constant.
- The average life (mean life) τ of a radioactive element is given by:
τ=1λ
2. Setting Up the Relationships:
- According to the problem, the half-life of element A is equal to the average life of element B. Therefore, we can write:
tA1/2=τB
3. Substituting the Formulas:
- Substitute the formulas for half-life and average life:
ln2λA=1λB
4. Cross-Multiplying:
- Cross-multiplying gives:
ln2=λAλB
5. Rearranging the Equation:
- Rearranging the equation to express λA in terms of λB:
λA=λB⋅ln2
6. Conclusion:
- This gives us the relationship between the decay constants of elements A and B:
λA=λB⋅ln2
Final Answer:
The correct relation is:
λA=λB⋅ln2
- The half-life t1/2 of a radioactive element is given by the formula:
t1/2=ln2λ
where λ is the decay constant.
- The average life (mean life) τ of a radioactive element is given by:
τ=1λ
- According to the problem, the half-life of element A is equal to the average life of element B. Therefore, we can write:
tA1/2=τB
- Substitute the formulas for half-life and average life:
ln2λA=1λB
- Cross-multiplying gives:
ln2=λAλB
- Rearranging the equation to express λA in terms of λB:
λA=λB⋅ln2
- This gives us the relationship between the decay constants of elements A and B:
λA=λB⋅ln2
The correct relation is:
λA=λB⋅ln2
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Calculate the ratio of half-life to the mean life of a radioactive sample . If λ be the decay constant of a radioactive sample.
A0.693B0.746C1/0.693D(0.693)2 - Question 2 - Select One
Two sources A and B have same power . The wavelength of radiation of A is λa and that of B is λb.The number of photons emitted per second by A and B are na and nb respectively, then
Aλa>λbBif λa>λb,na<nbCIf λa<λb,na<nbDif λa<λb,na=nb - Question 3 - Select One
Ac227 has a half-life of 22 years . The decays follows two parallel paths
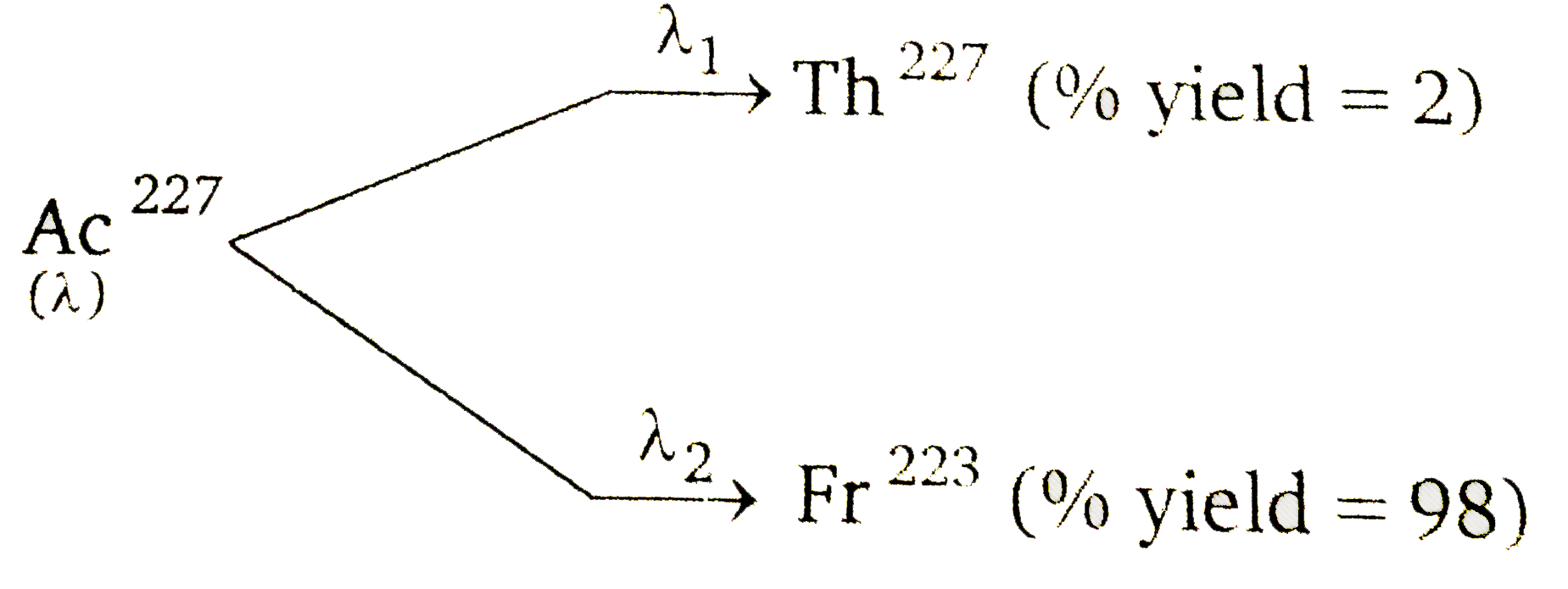
What are the decay constant (λ) for Th and Fr respectively ?A0.03087,0.00063B0.00063,0.03087C0.02,0.98DNone of these
The half-life period of a radioactive element x is same as the mean life time of another radioactive element y. Initially, both of them have the same number of atoms. Then,
(a) x and y have the same decay rate initially
(b) x and y decay at the same rate always
(c) y will decay at a faster rate than x
(d) x will decay at a faster rate than yView SolutionThe half life of 1 gm of a radioactive element of atomic weight M is T. The half life of M gm of the same element will be
View SolutionSample of two radioactive nuclides A and B are taken. λA and λB are the disintergration constants of A and B respectively. In which of the following cases, the two sample can simultaneously have the same decay rate at any time ?
View SolutionThe half-life of a radioactive sample A is same as the mean life of sample B. The number of atoms present initially in both the samples is same.
View SolutionSample of two radioactive nuclides A and B are taken. λA and λB are the disintergration constants of A and B respectively. In which of the following cases, the two sample can simultaneously have the same decay rate at any time ?
View Solution
