Question

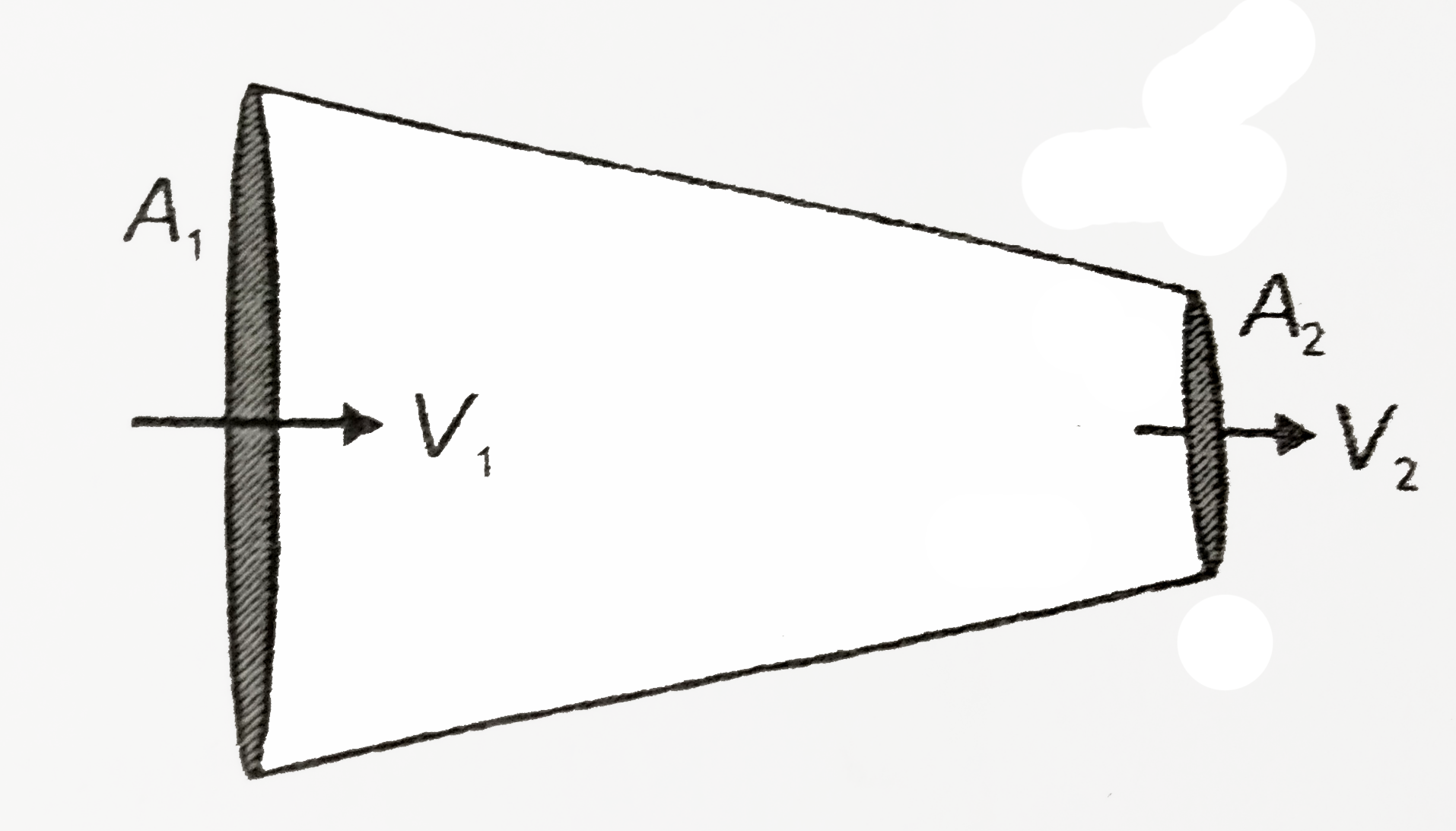
Glycrein of density $1.25\times {10}^{3}kgm6(-3)$ is flowing through the conical section of pipe.THe area of cross-section of the pipeat its end are $10c{m}^2$ and $5c{m}^2$ and pressure drop across its length is 3 Nm^(-2)$.therateofflowofglycer\in throughthe\pi peis$x times 10^(-5)m^(3) s^(-1) .The value of x is ______.

Explanation

To solve the problem, we need to find the rate of flow of glycerin through a conical pipe given the density, cross-sectional areas, and pressure drop. Let's break this down step by step.

Step 1: Understand the given data
- Density of glycerin, \( \rho = 1.25 \times 10^3 \, \text{kg/m}^3 \)
- Area at one end of the pipe, \( A_1 = 10 \, \text{cm}^2 = 10 \times 10^{-4} \, \text{m}^2 = 1 \times 10^{-3} \, \text{m}^2 \)
- Area at the other end of the pipe, \( A_2 = 5 \, \text{cm}^2 = 5 \times 10^{-4} \, \text{m}^2 \)
- Pressure drop, \( \Delta P = 3 \, \text{N/m}^2 \)

Step 2: Apply the continuity equation
Using the principle of conservation of mass, we can apply the continuity equation:
\( A_1 v_1 = A_2 v_2 \)
From this, we can express \( v_2 \) in terms of \( v_1 \):
\( v_2 = \frac{A_1}{A_2} v_1 = \frac{10 \times 10^{-4}}{5 \times 10^{-4}} v_1 = 2 v_1 \)

Step 3: Apply Bernoulli's equation
According to Bernoulli's equation, we have:
\( P_1 + \frac{1}{2} \rho v_1^2 = P_2 + \frac{1}{2} \rho v_2^2 \)
Rearranging gives us:
\( P_1 - P_2 = \frac{1}{2} \rho (v_2^2 - v_1^2) \)
Substituting \( \Delta P = P_1 - P_2 = 3 \, \text{N/m}^2 \) and \( v_2 = 2v_1 \):
\( 3 = \frac{1}{2} \rho ((2v_1)^2 - v_1^2) \)
\( 3 = \frac{1}{2} \rho (4v_1^2 - v_1^2) = \frac{1}{2} \rho (3v_1^2) \)
\( 3 = \frac{3}{2} \rho v_1^2 \)

Step 4: Solve for \( v_1^2 \)
Substituting the value of \( \rho \):
\( 3 = \frac{3}{2} (1.25 \times 10^3) v_1^2 \)
\( 3 = \frac{3 \times 1.25 \times 10^3}{2} v_1^2 \)
\( v_1^2 = \frac{3 \times 2}{3 \times 1.25 \times 10^3} = \frac{2}{1.25 \times 10^3} \)
\( v_1^2 = \frac{2}{1250} = \frac{1}{625} \quad \text{(m/s)}^2 \)
\( v_1 = \sqrt{\frac{1}{625}} = \frac{1}{25} = 0.04 \, \text{m/s} \)

Step 5: Calculate the rate of flow
The rate of flow \( Q \) is given by:
\( Q = A_1 v_1 \)
Substituting \( A_1 = 1 \times 10^{-3} \, \text{m}^2 \) and \( v_1 = 0.04 \, \text{m/s} \):
\( Q = (1 \times 10^{-3}) (0.04) = 4 \times 10^{-5} \, \text{m}^3/s \)

Step 6: Express in terms of \( x \)
The rate of flow is given as \( x \times 10^{-5} \, \text{m}^3/s \):
\( Q = 4 \times 10^{-5} \Rightarrow x = 4 \)

Final Answer
The value of \( x \) is 4.

---