A pole is vertically submerged in swimming pool, such that it gives a length of shadow 2.15 m within water when sunlight is incident at an angle of 30∘ with the surface of water. If swimming pool is filled to a height of 1.5 m, then the height of the pole above the water surface in centimeters is (nw = 4/3)
To solve the problem, we need to find the height of the pole above the water surface given the length of the shadow it casts underwater and the angle of sunlight incidence. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Geometry
The pole is submerged in water, and sunlight is hitting it at an angle of 30∘ to the surface of the water. The shadow of the pole underwater is 2.15m.
Step 2: Identify Angles
Since the sunlight is incident at 30∘, the angle of refraction in the water can be determined using Snell's law. The angle of incidence in air is 30∘ and the refractive index of water is μ=43.
Using Snell's law:
μ1sinθ1=μ2sinθ2
where μ1=1 (air), θ1=30∘, μ2=43, and θ2 is the angle in water.
Step 3: Calculate the Angle in Water
sin(30∘)=12
So,
1⋅12=43sinθ2
sinθ2=38
Step 4: Find the Height of the Pole Underwater
Let h be the height of the pole submerged in water. The length of the shadow x1 underwater can be expressed in terms of h and the angle θ2:
tan(θ2)=hx1
From the geometry, we know that:
x1+x2=2.15m
where x2 is the shadow above the water.
Step 5: Calculate the Height of the Pole
Using the relationship x1=htan(60∘) (since tan(60∘)=√3):
x1=h√3
Now, substituting x2 as 1.5tan(θ2):
x2=1.5⋅38=98
Now we can set up the equation:
h√3+98=2.15
Solving for h:
h√3=2.15−98
Convert 2.15 to eighths:
2.15=17.28
So,
h√3=17.28−98=8.28=1.025
Thus,
h=1.025√3≈0.591
Step 6: Calculate the Height Above Water
The total height of the pole is:
Total height=h+1.5
Convert h to centimeters:
Height above water=(h+1.5)×100≈(0.591+1.5)×100≈209.1cm
Final Answer
The height of the pole above the water surface is approximately 209.1 cm.
The pole is submerged in water, and sunlight is hitting it at an angle of 30∘ to the surface of the water. The shadow of the pole underwater is 2.15m.
Since the sunlight is incident at 30∘, the angle of refraction in the water can be determined using Snell's law. The angle of incidence in air is 30∘ and the refractive index of water is μ=43.
μ1sinθ1=μ2sinθ2
where μ1=1 (air), θ1=30∘, μ2=43, and θ2 is the angle in water.
sin(30∘)=12
So,
1⋅12=43sinθ2
sinθ2=38
Let h be the height of the pole submerged in water. The length of the shadow x1 underwater can be expressed in terms of h and the angle θ2:
tan(θ2)=hx1
From the geometry, we know that:
x1+x2=2.15m
where x2 is the shadow above the water.
Using the relationship x1=htan(60∘) (since tan(60∘)=√3):
x1=h√3
Now, substituting x2 as 1.5tan(θ2):
x2=1.5⋅38=98
Now we can set up the equation:
h√3+98=2.15
Solving for h:
h√3=2.15−98
Convert 2.15 to eighths:
2.15=17.28
So,
h√3=17.28−98=8.28=1.025
Thus,
h=1.025√3≈0.591
The total height of the pole is:
Total height=h+1.5
Convert h to centimeters:
Height above water=(h+1.5)×100≈(0.591+1.5)×100≈209.1cm
The height of the pole above the water surface is approximately 209.1 cm.
Topper's Solved these Questions
Similar Questions
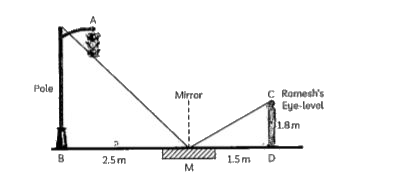
If the distance of Ramesh and the pole from the mirror are 2.5 m and 1.5 m respectively, then the height of the pole is:
View SolutionA pole of length 1.00 m stands half dipped in a swimming pool with water level 50.0 cm higher than the bed. The refractive index of water is 1.33 and sunlight is coming at an angle of 45° with the vertical. Find the length of the shadow of the pole on the bed.
View Solution
Knowledge Check
A bird is flying 3m above the surface of water. To a fish underwater, the height of the bird from the water surface appears to be
A2.25mB3.33mC4mD4/3mArea of curved surface of a cylindrical pole is 264m2 and its volume is 1848m3.What is the height of the pole? {use pai=22/7}
A4mB3mC5mD6mA pole 5 m high is situated on a horizontal surface. Sun rays are incident at an angle 30∘ with the vertical. The size of shadow on horizontal surface is
A5 cmB5√3 mC10√3 mDnone of these
A swimming pool is 50 m in length,30 m in breadth and 2.5 m in depth. Find the cost of cementing its floor and walls at the rate of Rs 27 per square metre.
View SolutionA hill, 101(13) m in height, has 14 th of its height under water. What is the height of the hill visible above the water?
View SolutionA pole 5 m high is situated on a horizontal surface. Sun rays are incident at an angle 30∘ with the vertical. The size of shadow on horizontal surface is
View SolutionA fish in water sees an object which is 24cm above the surface of water. The height of the object above the surface of water that will appear to the flash is (μ=4/3)
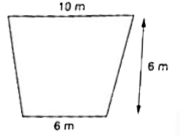
View SolutionIn the adjoining figure the cross-section of a swimming pool is shown . If the length of the swimming pool is 120 m then the amount of water it can hold is :
View Solution
