For the adsorption of hydrogen on platinum, the activation energy is 30kJmol–1 and for the adsorption of hydrogen on nickel, the activation energy is 41.4kJmol–1 . The logarithm of the ratio of the rates of chemisorption on equal areas of the metals at 300 K is ______ (Nearest integer)
Given : In 10 = 2.3
R=8.3JK–1mol–1
To solve the problem, we need to find the logarithm of the ratio of the rates of chemisorption of hydrogen on platinum and nickel at 300 K. We will use the Arrhenius equation to derive the required logarithmic ratio.
1. Identify the Activation Energies:
- For platinum (Pt), the activation energy Ea1=30kJ/mol.
- For nickel (Ni), the activation energy Ea2=41.4kJ/mol.
2. Convert Activation Energies to Joules:
Since the gas constant R is given in Joules, we need to convert the activation energies from kJ/mol to J/mol:
Ea1=30kJ/mol=30×1000J/mol=30000J/mol
Ea2=41.4kJ/mol=41.4×1000J/mol=41400J/mol
3. Write the Arrhenius Equation:
The rate constant k is given by:
k=Ae−EaRT
where A is the pre-exponential factor, Ea is the activation energy, R is the gas constant, and T is the temperature in Kelvin.
4. Calculate the Ratio of Rate Constants:
The ratio of the rate constants k2 for nickel to k1 for platinum can be expressed as:
k2k1=Ae−Ea2RTAe−Ea1RT=e−Ea2−Ea1RT
5. Take the Natural Logarithm:
Taking the natural logarithm of both sides gives:
ln(k2k1)=−Ea2−Ea1RT
6. Convert to Logarithm Base 10:
To convert from natural logarithm to base 10 logarithm, we use the conversion factor ln(x)=2.303log10(x):
log10(k2k1)=−(Ea2−Ea1)2.303RT
7. Substitute Values:
Substituting the values of Ea1, Ea2, R, and T:
log10(k2k1)=−(41400−30000)2.303×8.3×300
=−114002.303×8.3×300
8. Calculate the Denominator:
First, calculate 2.303×8.3×300:
2.303×8.3≈19.1169
19.1169×300≈5735.07
9. Final Calculation:
Now calculate:
log10(k2k1)=−114005735.07≈−1.989
10. Round to Nearest Integer:
The nearest integer to −1.989 is −2.
Final Answer:
The logarithm of the ratio of the rates of chemisorption on equal areas of the metals at 300 K is −2.
- For platinum (Pt), the activation energy Ea1=30kJ/mol.
- For nickel (Ni), the activation energy Ea2=41.4kJ/mol.
Since the gas constant R is given in Joules, we need to convert the activation energies from kJ/mol to J/mol:
Ea1=30kJ/mol=30×1000J/mol=30000J/mol
Ea2=41.4kJ/mol=41.4×1000J/mol=41400J/mol
The rate constant k is given by:
k=Ae−EaRT
where A is the pre-exponential factor, Ea is the activation energy, R is the gas constant, and T is the temperature in Kelvin.
The ratio of the rate constants k2 for nickel to k1 for platinum can be expressed as:
k2k1=Ae−Ea2RTAe−Ea1RT=e−Ea2−Ea1RT
Taking the natural logarithm of both sides gives:
ln(k2k1)=−Ea2−Ea1RT
To convert from natural logarithm to base 10 logarithm, we use the conversion factor ln(x)=2.303log10(x):
log10(k2k1)=−(Ea2−Ea1)2.303RT
Substituting the values of Ea1, Ea2, R, and T:
log10(k2k1)=−(41400−30000)2.303×8.3×300
=−114002.303×8.3×300
First, calculate 2.303×8.3×300:
2.303×8.3≈19.1169
19.1169×300≈5735.07
Now calculate:
log10(k2k1)=−114005735.07≈−1.989
The nearest integer to −1.989 is −2.
The logarithm of the ratio of the rates of chemisorption on equal areas of the metals at 300 K is −2.
Topper's Solved these Questions
Similar Questions
The activation energy for the decomposition of hydrogen iodide at 581 K is 209.5 kJ mol–1. Calculate the fraction of molecules having energy equal to activation energy.
View SolutionThe activation energy of a first order reaction at 300 K is 60 kJ mol−1. In the presence of a catalyst, the activation energy is lowered to 50 kJ mol−1 at the same teperature. How many times the rate of reaction will change ?
View Solution
Knowledge Check
In an exothermic reaction X→Y, the activation energy is 100kJmol−1 of X. The enthalphy of the reaction is −140kJmol−1. The activation energy of the reverse reaction Y→X is
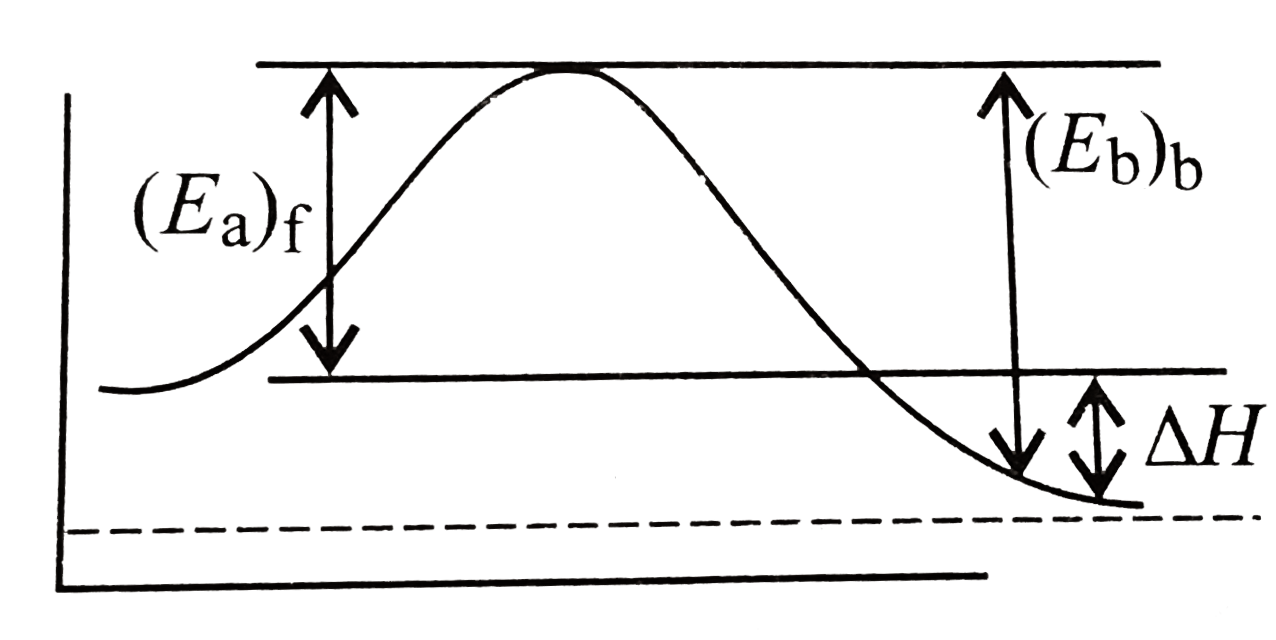 A40kJmol−1B340kJmol−1C240kJmol−1D100kJmol−1
A40kJmol−1B340kJmol−1C240kJmol−1D100kJmol−1If the activation enery for the forward reaction is 150kJ mol−1 and that of the reverse reaction is 260kJ mol−1. What is the ethalpy change for the reaction ?
A410 kJ mol−1B−110 kJ mol−1C110 kJ mol−1D−410 kJ mol−1If the activation enery for the forward reaction is 150kJ mol−1 and that of the reverse reaction is 260kJ mol−1. What is the ethalpy change for the reaction ?
A410 kJ mol−1B−110kJmol−1C110 kJ mol−1D−410kJmol−1
The activation energy of a first order reaction at 300K is kJmol−1. In the presence of a catalyst, the activation energy gets lowered to 50kJmol−1 at 300K. How many times the reaction rate change in the presence of a catalyst at the same temperature ?
View SolutionAn endothermic reaction A ⇔ B has an activation energy as x kJ mol−1 of A. If energy change of the reaction is y kJ, the activation energy of the reverse reaction is
View SolutionThe activation energy of a reaction is 58.3 kJ mol−1. The ratio of rate constants at 305 K and 300 K is about (R= 8.3 J K−1mol−1)
View SolutionThe approximate energy (kJmol−1) of hydrogen bonding is
View SolutionAn exothermic reaction A → B has an activation energy of X kJ mol−1 of A. If the energy change in the reaction is Y kJ, then the activation energy of the backward reaction will be
View Solution
