The distance between two plates of a capacitor is d and its capacitance is C1, when air is the medium between the plates. If a metal sheet of thickness 2d3 and of the same area as plate is introduced between the plates, the capacitance of the capacitor becomes C2. The ratio C2C1 is
0.12569444444444
0.084027777777778
0.16736111111111
0.042361111111111
To solve the problem, we need to find the ratio of the capacitance of the capacitor after introducing a metal sheet between the plates to the original capacitance when air is the medium.
1. Understanding Capacitance:
The capacitance C of a parallel plate capacitor is given by the formula:
C=Aϵd
where A is the area of the plates, ϵ is the permittivity of the medium between the plates, and d is the distance between the plates.
2. Capacitance with Air:
When the medium is air, the capacitance C1 can be expressed as:
C1=Aϵ0d
where ϵ0 is the permittivity of free space (air).
3. Introducing the Metal Sheet:
A metal sheet of thickness 2d3 is introduced between the plates. This effectively divides the capacitor into two capacitors in series:
- The first capacitor has a thickness of d−2d3=d3 with air as the medium.
- The second capacitor is the metal sheet, which has an infinite capacitance (since the potential difference across a conductor is zero).
4. Capacitance of the Air Gap:
The capacitance Cair of the air gap (thickness d3) is given by:
Cair=Aϵ0d3=3Aϵ0d
5. Capacitance of the Metal Sheet:
The capacitance Cmetal of the metal sheet is effectively infinite, but since it is in series with the air gap, we can treat the total capacitance C2 as:
1C2=1Cair+1Cmetal≈1Cair(since Cmetal→∞)
Thus, we have:
C2≈Cair=3Aϵ0d
6. Finding the Ratio:
Now, we can find the ratio C2C1:
C2C1=3Aϵ0dAϵ0d=3
Final Answer:
The ratio C2C1 is 3.
The capacitance C of a parallel plate capacitor is given by the formula:
C=Aϵd
where A is the area of the plates, ϵ is the permittivity of the medium between the plates, and d is the distance between the plates.
When the medium is air, the capacitance C1 can be expressed as:
C1=Aϵ0d
where ϵ0 is the permittivity of free space (air).
A metal sheet of thickness 2d3 is introduced between the plates. This effectively divides the capacitor into two capacitors in series:
- The first capacitor has a thickness of d−2d3=d3 with air as the medium.
- The second capacitor is the metal sheet, which has an infinite capacitance (since the potential difference across a conductor is zero).
The capacitance Cair of the air gap (thickness d3) is given by:
Cair=Aϵ0d3=3Aϵ0d
The capacitance Cmetal of the metal sheet is effectively infinite, but since it is in series with the air gap, we can treat the total capacitance C2 as:
1C2=1Cair+1Cmetal≈1Cair(since Cmetal→∞)
Thus, we have:
C2≈Cair=3Aϵ0d
Now, we can find the ratio C2C1:
C2C1=3Aϵ0dAϵ0d=3
The ratio C2C1 is 3.
Topper's Solved these Questions
Similar Questions
Two metal plates form a parallel plate capacitor. The distance between the plates is d. A metal sheet of thickness d/2 and of the same area is indroduced between the plates. What is the ratio of the capacitances in the two cases?
View SolutionThe distance between the plates of a parallel plate capacitor is 'd'. The capacitance of the capacitor gets doubled when a metal plate of thicknessd2 is placed between the plates.
View Solution
Knowledge Check
The capacitance of a parallel plate condenser with a separation of 4 mm between the plates is 7μF. If a mica sheet (K=6) of thickness 2 mm and of the same area is introduced betwenn the plates, its capacitance will be
A6μFB9μFC12μFD15μFTwo metal plates form a parallel plate condenser. The distance between the plates in d. Now a metal plate of thickness d/2 and of same area is inserted completely between the plates, the capacitance
Aremains unchangedBis doubledCis halvedDreduced to one fourthA metal plate of thickness half the separation between the capacitor plates of capacitance C is inserted. The new capacitance is.
ACBC/2CzeroD2C
A metal slab of thickness, equal to half the distance between the plates is introduced between the plates of a parallel plate capacitor as shown. Find its capacity.
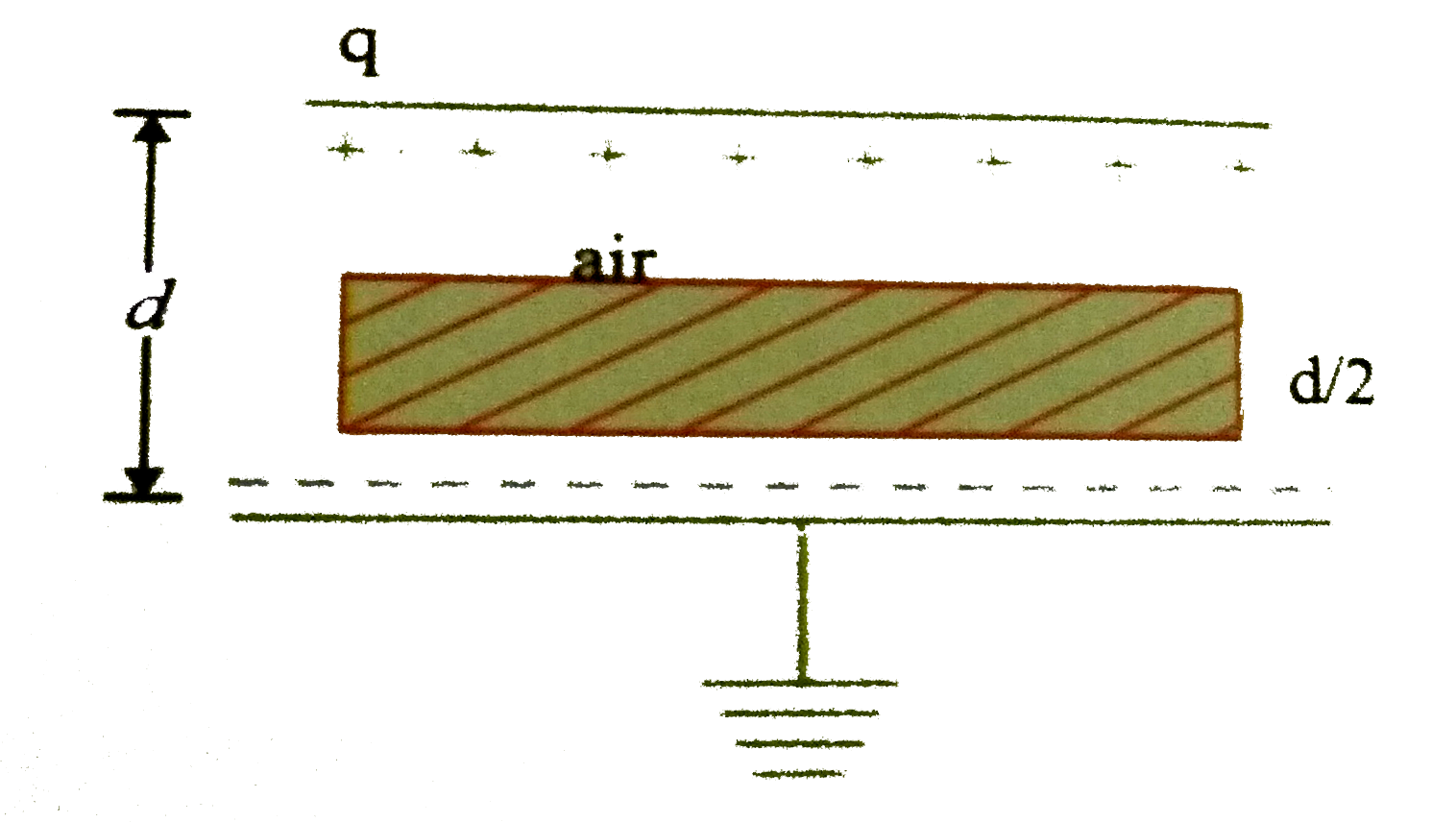 .
.
View SolutionIn a parallel plate capacitor of capacitance C, a metal sheet is inserted between the plates, parallel to them. If the thickness of the sheet is half of the separation between the plates. The capacitance will be
View SolutionA parallel plate capacitor has a capacitance of 60 PF, when the plates of the capacitor and separated by a distance d. if a metal plate of thickness t=d3 is introduced between the plates, the capacitance will be
View SolutionThe separation between the plates of a parallel plate capacitor is d and the area of each plate is A. iff a dielectric slab of thickness x and dielectric constant K is introduced between the plates, then the capacitance will be
View SolutionA sheet of aluminium foil of negligible thickness is placed between the plates of a capacitor of capacitance C as shown in the figure then capacitance of capacitor becomes

View Solution