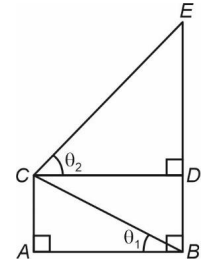
In the figure $θ_{1} + θ_{2} = \frac{π}{2}$ and $\sqrt{3} (B E) = 4 (A B)$ . If the area of $△ C A B$ is $2 \sqrt{3} - 3 u n i t^{2}$ , when $\frac{θ_{2}}{θ_{1}}$ is the largest, then the perimeter of $△ C E D$ is equal to

Video Solution

Answer

Step by step video solution for In the figure theta_1+theta_2=pi/2 and sqrt3(BE)=4(AB). If the area of triangleCAB is 2sqrt3-3 unit^2, when (theta_2)/(theta_1) is the largest, then the perimeter of triangleCED is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
If ${sin θ}_{1} + {sin θ}_{2} + {sin θ}_{3} = 3$ then ${cos θ}_{1} + {cos θ}_{2} + {cos θ}_{3}$ is equal to
A3
B2
C1
D0
Question 2 - Select One or More
If $r sin θ = \sqrt{3}, r + 4 sin θ = 2 (\sqrt{3} + 1), 0 \leq θ \leq 2 π$ , then $θ$ =
A $30^{\circ}$
B $60^{\circ}$
C $120^{\circ}$
D $150^{\circ}$
Question 3 - Select One
If $3 {cos}^{2} θ - 2 \sqrt{3} sin θ . cos θ - 3 {sin}^{2} θ = 0$ , then $θ$ =
A $\frac{n π}{2} + \frac{π}{6}$
B $\frac{n π}{2} - \frac{π}{6}$
C $\frac{n π}{2} + \frac{π}{3}$
D $\frac{n π}{2} - \frac{π}{3}$

JEE MAINS PREVIOUS YEAR-JEE MAIN 2023-Question

Home
Ask Doubt
Profile

In the figure θ1+θ2=π2 and √3(BE)=4(AB). If the area of △CAB is 2√3−3unit2, when θ2θ1 is the largest, then the perimeter of △CED is equal to

Topper's Solved these Questions

Similar Questions

Knowledge Check

If sinθ1+sinθ2+sinθ3=3 then cosθ1+cosθ2+cosθ3 is equal to

If rsinθ=√3,r+4sinθ=2(√3+1),0≤θ≤2π, then θ=

If 3cos2θ−2√3sinθ.cosθ−3sin2θ=0, then θ =

JEE MAINS PREVIOUS YEAR-JEE MAIN 2023-Question

In the figure $θ_{1} + θ_{2} = \frac{π}{2}$ and $\sqrt{3} (B E) = 4 (A B)$ . If the area of $△ C A B$ is $2 \sqrt{3} - 3 u n i t^{2}$ , when $\frac{θ_{2}}{θ_{1}}$ is the largest, then the perimeter of $△ C E D$ is equal to

If ${sin θ}_{1} + {sin θ}_{2} + {sin θ}_{3} = 3$ then ${cos θ}_{1} + {cos θ}_{2} + {cos θ}_{3}$ is equal to

If $r sin θ = \sqrt{3}, r + 4 sin θ = 2 (\sqrt{3} + 1), 0 \leq θ \leq 2 π$ , then $θ$ =

If $3 {cos}^{2} θ - 2 \sqrt{3} sin θ . cos θ - 3 {sin}^{2} θ = 0$ , then $θ$ =