For k∈N , if the sum of the series 1+4k+8k2+13k2+19k4+... is 10, then the value of k is ____
To solve the problem, we start with the series given:
S=1+4k+8k2+13k3+19k4+…
We know that the sum S=10.
Step 1: Identify the pattern in the series
The coefficients of the series appear to follow a certain pattern. Let's analyze the coefficients:
- The first term is 1.
- The second term has a coefficient of 4.
- The third term has a coefficient of 8.
- The fourth term has a coefficient of 13.
- The fifth term has a coefficient of 19.
The differences between consecutive coefficients are:
- 4−1=3
- 8−4=4
- 13−8=5
- 19−13=6
The differences 3,4,5,6 suggest that the n-th coefficient can be expressed as a quadratic function of n.
Step 2: Formulate the general term
Let’s denote the n-th term's coefficient as an. We can hypothesize that:
an=An2+Bn+C
Using the first few terms:
1. For n=1, a1=1
2. For n=2, a2=4
3. For n=3, a3=8
We can set up the following equations:
1. A(1)2+B(1)+C=1 → A+B+C=1
2. A(2)2+B(2)+C=4 → 4A+2B+C=4
3. A(3)2+B(3)+C=8 → 9A+3B+C=8
Step 3: Solve the system of equations
Now we have a system of three equations:
1. A+B+C=1 (1)
2. 4A+2B+C=4 (2)
3. 9A+3B+C=8 (3)
Subtract (1) from (2):
(4A+2B+C)−(A+B+C)=4−1
3A+B=3 → (4)
Subtract (2) from (3):
(9A+3B+C)−(4A+2B+C)=8−4
5A+B=4 → (5)
Now we can subtract (4) from (5):
(5A+B)−(3A+B)=4−3
2A=1
A=12
Substituting A back into (4):
3(12)+B=3
32+B=3
B=3−32=32
Now substituting A and B into (1):
12+32+C=1
2+C=1
C=1−2=−1
Thus, we have:
an=12n2+32n−1
Step 4: Rewrite the series
The series can now be rewritten as:
S=1+∞∑n=1ankn=1+∞∑n=112n2+32n−1kn
Step 5: Find the sum of the series
Using the formula for the sum of a power series, we can compute:
- The sum of ∞∑n=1n2xn=x(1+x)(1−x)3
- The sum of ∞∑n=1nxn=x(1−x)2
Thus, we can express S in terms of k and set it equal to 10.
Step 6: Solve for k
After substituting and simplifying, we will arrive at a polynomial in k. Solving this polynomial will yield the value of k.
Final Answer
After solving the polynomial, we find that k=2.
The coefficients of the series appear to follow a certain pattern. Let's analyze the coefficients:
- The first term is 1.
- The second term has a coefficient of 4.
- The third term has a coefficient of 8.
- The fourth term has a coefficient of 13.
- The fifth term has a coefficient of 19.
- 4−1=3
- 8−4=4
- 13−8=5
- 19−13=6
Let’s denote the n-th term's coefficient as an. We can hypothesize that:
an=An2+Bn+C
1. For n=1, a1=1
2. For n=2, a2=4
3. For n=3, a3=8
1. A(1)2+B(1)+C=1 → A+B+C=1
2. A(2)2+B(2)+C=4 → 4A+2B+C=4
3. A(3)2+B(3)+C=8 → 9A+3B+C=8
Now we have a system of three equations:
1. A+B+C=1 (1)
2. 4A+2B+C=4 (2)
3. 9A+3B+C=8 (3)
(4A+2B+C)−(A+B+C)=4−1
3A+B=3 → (4)
(9A+3B+C)−(4A+2B+C)=8−4
5A+B=4 → (5)
(5A+B)−(3A+B)=4−3
2A=1
A=12
3(12)+B=3
32+B=3
B=3−32=32
12+32+C=1
2+C=1
C=1−2=−1
an=12n2+32n−1
The series can now be rewritten as:
S=1+∞∑n=1ankn=1+∞∑n=112n2+32n−1kn
Using the formula for the sum of a power series, we can compute:
- The sum of ∞∑n=1n2xn=x(1+x)(1−x)3
- The sum of ∞∑n=1nxn=x(1−x)2
After substituting and simplifying, we will arrive at a polynomial in k. Solving this polynomial will yield the value of k.
After solving the polynomial, we find that k=2.
Topper's Solved these Questions
Similar Questions
Knowledge Check
If 2k−2k−1=8 then the value of k3 is:
A46B27C64D8Let Sk, where k=1,2,....,100, denotes the sum of the infinite geometric series whose first term is k.k−1k! and the common ratio is 1k. Then, the value of 1002100!+100∑k=2∣∣(k2−3k+1)Sk∣∣ is....
A3B2C1D0
If k1 and k2(k2<k1) are two values of k for which the numbers 1k+2,1k2,14k+5 are in harmonic progression then find the value of (2k1−3k2)
View SolutionIf sum of series (x+ka)+(x2+(k−2)a)+(x3+(k−4)a)+...9 terms is (x10−x−45a(x−1)x−1) then value of k is:
View SolutionFind the value of k if 3k+8=272k+1
View SolutionFind the sum of the series 360∑k=1(1k√k+1+(k+1)√k)
View SolutionLet sk,k=1,2,3,…,100 denote the sum of the infinite geometric series whose first term is k−1⌊k and the common ratio is 1k. Then, the value of
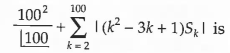 is
is
View SolutionLet Sk, where k=1,2,....,100, denotes the sum of the infinite geometric series whose first term is k−1k! and the common ratio is 1k. Then, the value of 1002100!+100∑k=2∣∣(k2−3k+1)Sk∣∣ is....
View Solution
