Given below are two statements:
Statement I:According to Bohr's model of hydrogen atomthe angular momentum of an electron in a given stationary state is quantised.
Statement II:The concept of electron in Bohr's orbit. violates the Heisenberg uncertainty principle.
In the light of the above statements, choose the most appropriate answer from the options given below:
Both Statement I and Statement II are correct
Both Statement I and Statement II are incorrect
Statement I is correct but Statement II is incorrect
Statement I is incorrect but Statement II is correct
To solve the problem, we need to analyze both statements provided in the question regarding the Bohr model of the hydrogen atom and the Heisenberg uncertainty principle.
1. Understanding Statement I:
- According to Bohr's model, the angular momentum (L) of an electron in a hydrogen atom is quantized. This means that the angular momentum can only take on certain discrete values.
- The formula for the angular momentum in a stationary state is given by:
L=nh2π
where n is the principal quantum number (n = 1, 2, 3, ...), and h is Planck's constant.
- Therefore, Statement I is correct.
2. Understanding Statement II:
- The Heisenberg uncertainty principle states that it is impossible to simultaneously know both the position and momentum of an electron with arbitrary precision. This implies that if we know the position of an electron very precisely, its momentum becomes uncertain and vice versa.
- In Bohr's model, electrons are depicted as moving in fixed orbits with a definite radius and velocity, which suggests that both position and momentum can be known precisely. This contradicts the Heisenberg uncertainty principle.
- Therefore, Statement II is also correct.
3. Conclusion:
- Since both statements are correct, the most appropriate answer is that both Statement I and Statement II are correct.
Final Answer:
Both Statement I and Statement II are correct.
- According to Bohr's model, the angular momentum (L) of an electron in a hydrogen atom is quantized. This means that the angular momentum can only take on certain discrete values.
- The formula for the angular momentum in a stationary state is given by:
L=nh2π
where n is the principal quantum number (n = 1, 2, 3, ...), and h is Planck's constant.
- Therefore, Statement I is correct.
- The Heisenberg uncertainty principle states that it is impossible to simultaneously know both the position and momentum of an electron with arbitrary precision. This implies that if we know the position of an electron very precisely, its momentum becomes uncertain and vice versa.
- In Bohr's model, electrons are depicted as moving in fixed orbits with a definite radius and velocity, which suggests that both position and momentum can be known precisely. This contradicts the Heisenberg uncertainty principle.
- Therefore, Statement II is also correct.
- Since both statements are correct, the most appropriate answer is that both Statement I and Statement II are correct.
Both Statement I and Statement II are correct.
Topper's Solved these Questions
Similar Questions
Match List-I with List -II

Choose the most appropriate answer from the options given below:
View SolutionMatch List I with List II :
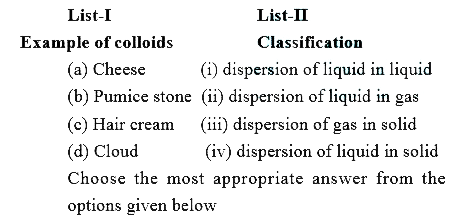
Choose the most appropriate answer from the options given below
View SolutionMatch list - I with List - II :
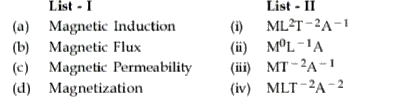
Choose the most appropriate answer from the options given below :
View SolutionMatch List - I with List -II

Choose the most appropriate answer from the options given below :
View SolutionMatch List-I with List-II :
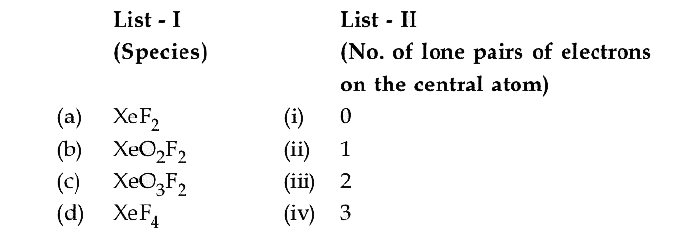
Choose the most appropriate answer from the options given below :
View SolutionMatch List-I with List-II :

Choose the most appropriate answer from the options given below :
View SolutionMatch List -I with List-II :
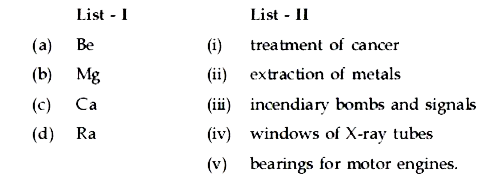
Choose the most appropriate answer from the option given below:
View SolutionMatch List - I with List - II
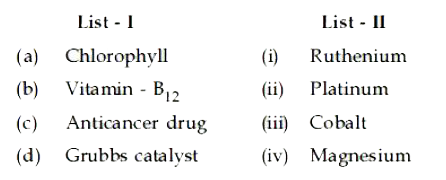
Choose the most appropriate answer from the options given below :
View SolutionMatch List - I with List - II.

Choose the most appropriate answer from the options given below :
View SolutionMatch List - I with List - II.
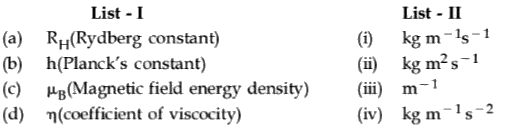
Choose the most appropriate answer from the options given below :
View Solution
