For any real number x, Let [x] denote the largest integer less than or equal to x. The value of 9∫90[√10xx+1]dx
To solve the integral 9∫90(√10xx+1)dx, where (x) denotes the greatest integer less than or equal to x, we will follow these steps:
Step 1: Analyze the function inside the integral
We start by analyzing the function √10xx+1. We need to determine its behavior as x varies from 0 to 9.
Step 2: Find the range of √10xx+1
- At x=0:
√10⋅00+1=√0=0
- At x=9:
√10⋅99+1=√9010=√9=3
Thus, as x varies from 0 to 9, √10xx+1 varies from 0 to 3.
Step 3: Determine the intervals for the greatest integer function
The greatest integer function (y) will take on integer values based on the value of y:
- (y)=0 when 0≤y<1
- (y)=1 when 1≤y<2
- (y)=2 when 2≤y<3
Step 4: Find the values of x for each interval
1. For (y)=0:
√10xx+1<1⟹10xx+1<1⟹10x<x+1⟹9x<1⟹x<19
Therefore, for 0≤x<19, (y)=0.
2. For (y)=1:
1≤√10xx+1<2⟹1≤10xx+1<4
- From 1≤10xx+1:
x+1≤10x⟹9x≥1⟹x≥19
- From 10xx+1<4:
10x<4(x+1)⟹10x<4x+4⟹6x<4⟹x<23
Therefore, for 19≤x<23, (y)=1.
3. For (y)=2:
2≤√10xx+1<3⟹4≤10xx+1<9
- From 4≤10xx+1:
x+1≤10x/4⟹4x+4≤10x⟹6x≥4⟹x≥23
- From 10xx+1<9:
10x<9(x+1)⟹10x<9x+9⟹x<9
Therefore, for 23≤x<9, (y)=2.
Step 5: Set up the integral based on intervals
Now we can set up the integral:
9∫90(√10xx+1)dx=9(∫1900dx+∫23191dx+∫9232dx)
Step 6: Evaluate the integrals
1. ∫1900dx=0
2. ∫23191dx=(x)2319=23−19=69−19=59
3. ∫9232dx=2(x)923=2(9−23)=2(273−23)=2⋅253=503
Step 7: Combine the results
Now, combining these results:
9(0+59+503)=9(59+1509)=9⋅1559=155
Final Answer
The value of 9∫90(√10xx+1)dx is 155.
We start by analyzing the function √10xx+1. We need to determine its behavior as x varies from 0 to 9.
- At x=0:
√10⋅00+1=√0=0
- At x=9:
√10⋅99+1=√9010=√9=3
Thus, as x varies from 0 to 9, √10xx+1 varies from 0 to 3.
The greatest integer function (y) will take on integer values based on the value of y:
- (y)=0 when 0≤y<1
- (y)=1 when 1≤y<2
- (y)=2 when 2≤y<3
1. For (y)=0:
√10xx+1<1⟹10xx+1<1⟹10x<x+1⟹9x<1⟹x<19
Therefore, for 0≤x<19, (y)=0.
1≤√10xx+1<2⟹1≤10xx+1<4
- From 1≤10xx+1:
x+1≤10x⟹9x≥1⟹x≥19
- From 10xx+1<4:
10x<4(x+1)⟹10x<4x+4⟹6x<4⟹x<23
Therefore, for 19≤x<23, (y)=1.
2≤√10xx+1<3⟹4≤10xx+1<9
- From 4≤10xx+1:
x+1≤10x/4⟹4x+4≤10x⟹6x≥4⟹x≥23
- From 10xx+1<9:
10x<9(x+1)⟹10x<9x+9⟹x<9
Therefore, for 23≤x<9, (y)=2.
Now we can set up the integral:
9∫90(√10xx+1)dx=9(∫1900dx+∫23191dx+∫9232dx)
1. ∫1900dx=0
2. ∫23191dx=(x)2319=23−19=69−19=59
3. ∫9232dx=2(x)923=2(9−23)=2(273−23)=2⋅253=503
Now, combining these results:
9(0+59+503)=9(59+1509)=9⋅1559=155
The value of 9∫90(√10xx+1)dx is 155.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Let [x] denote the greatest integer less than or equal to x. Then, ∫1.50[x]dx=?
A12B32C2D3Let [x] denote the greatest integer less than or equal to x. Then, ∫−11[x]dx=?
A−1B0C12D2For a real number x let [x] denote the largest intger less than or equal to x. The smalleset positive integer n for which the integer ∫n1[x][√x]dx exceeds 60 is-
A8B9C10D[602/3]
For a real number x let [x] denote the largest number less than or equal to x. For x∈R let f (x)=[x] sinπx. Then
View SolutionFor any real number x, let [x] denotes the largest integer less than or equal to x.Let f be a real valued function defined on the interval[-10,10] by
f(x)={(x−[x])<br>(1+[x]−x)}
Then, the value of π210∫10−10 f(x) cos π x dx is
View SolutionFor a real number x let [x] denote the largest integer less than or equal to x and {x}=x−[x]. The possible integer value of n for which ∫n1[x]{x}dx exceeds 2013 is
View SolutionFor any real number x, let [x]= largest integer less than or equalto x. Let f be a real valued function defined on the interval[−10,10] by
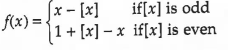 Then, the value of (π10)2(∫10−10f(x)cosπxdx is
Then, the value of (π10)2(∫10−10f(x)cosπxdx is
View SolutionFor a real number x let [x] denote the largest integer less than or equal to x and {x}=x−[x]. The possible integer value of n for which ∫n1[x]{x}dx exceeds 2013 is
View Solution
