The bob of a pendulum was released from a horizontal position. The length of the pendulum is 10m. If it dissipates 10% of its initial energy against air resistance, the speed with which the bob arrives at the lowest point is : [Use, g:10ms–2]
6√5ms−1
5√6ms−1
5√5ms−1
2√5ms−1
The correct Answer is:A
To solve the problem, we will use the principle of conservation of energy. The pendulum bob is released from a horizontal position, which means it starts with potential energy and no kinetic energy. As it swings down, some of this potential energy is converted into kinetic energy, but we also have to account for the energy dissipated due to air resistance.
1. Identify Initial Potential Energy:
The initial potential energy (PE) when the bob is at the horizontal position (height = length of the pendulum) is given by:
PE=mgh
where:
- m = mass of the bob (we will see it cancels out)
- g=10m/s2 (acceleration due to gravity)
- h=10m (length of the pendulum)
So,
PE=mg⋅10
2. Calculate Energy Dissipated:
Since 10% of the energy is dissipated due to air resistance, the energy available for conversion to kinetic energy (KE) is:
KE=90% of PE=0.9⋅PE=0.9⋅mg⋅10
3. Set Up the Energy Conservation Equation:
At the lowest point of the swing (point B), all the potential energy that is not dissipated will be converted into kinetic energy. The potential energy at the lowest point is zero, so we have:
0.9⋅mg⋅10=12mv2
4. Cancel the Mass m:
Since m appears on both sides of the equation, we can cancel it out:
0.9⋅g⋅10=12v2
5. Substitute the Value of g:
Now substituting g=10m/s2:
0.9⋅10⋅10=12v2
This simplifies to:
90=12v2
6. Solve for v2:
Multiply both sides by 2:
180=v2
7. Take the Square Root:
Finally, take the square root to find v:
v=√180=√36⋅5=6√5m/s
Final Answer:
The speed with which the bob arrives at the lowest point is 6√5m/s.
The initial potential energy (PE) when the bob is at the horizontal position (height = length of the pendulum) is given by:
PE=mgh
where:
- m = mass of the bob (we will see it cancels out)
- g=10m/s2 (acceleration due to gravity)
- h=10m (length of the pendulum)
PE=mg⋅10
Since 10% of the energy is dissipated due to air resistance, the energy available for conversion to kinetic energy (KE) is:
KE=90% of PE=0.9⋅PE=0.9⋅mg⋅10
At the lowest point of the swing (point B), all the potential energy that is not dissipated will be converted into kinetic energy. The potential energy at the lowest point is zero, so we have:
0.9⋅mg⋅10=12mv2
Since m appears on both sides of the equation, we can cancel it out:
0.9⋅g⋅10=12v2
Now substituting g=10m/s2:
0.9⋅10⋅10=12v2
This simplifies to:
90=12v2
Multiply both sides by 2:
180=v2
Finally, take the square root to find v:
v=√180=√36⋅5=6√5m/s
The speed with which the bob arrives at the lowest point is 6√5m/s.
Topper's Solved these Questions
Similar Questions
The string of a pendulum is 2.0m long. The bob is pulled sideways so that the string becomes horizontal and then the bob is released. What is the speed with which the bob arrives at the lowest point ? Assume theat 10% of initial energy is dissipated against air resistance. Take g=10m/s2
View SolutionThe bob A of a simple pendulum is released from a horizontal position A as shownin in figure. If the length of the pendulum is 1.5m , what is the speed with which the bob arrives at the lowermost point B, given that it dissipates 5% of its initial energy against air resistance ?
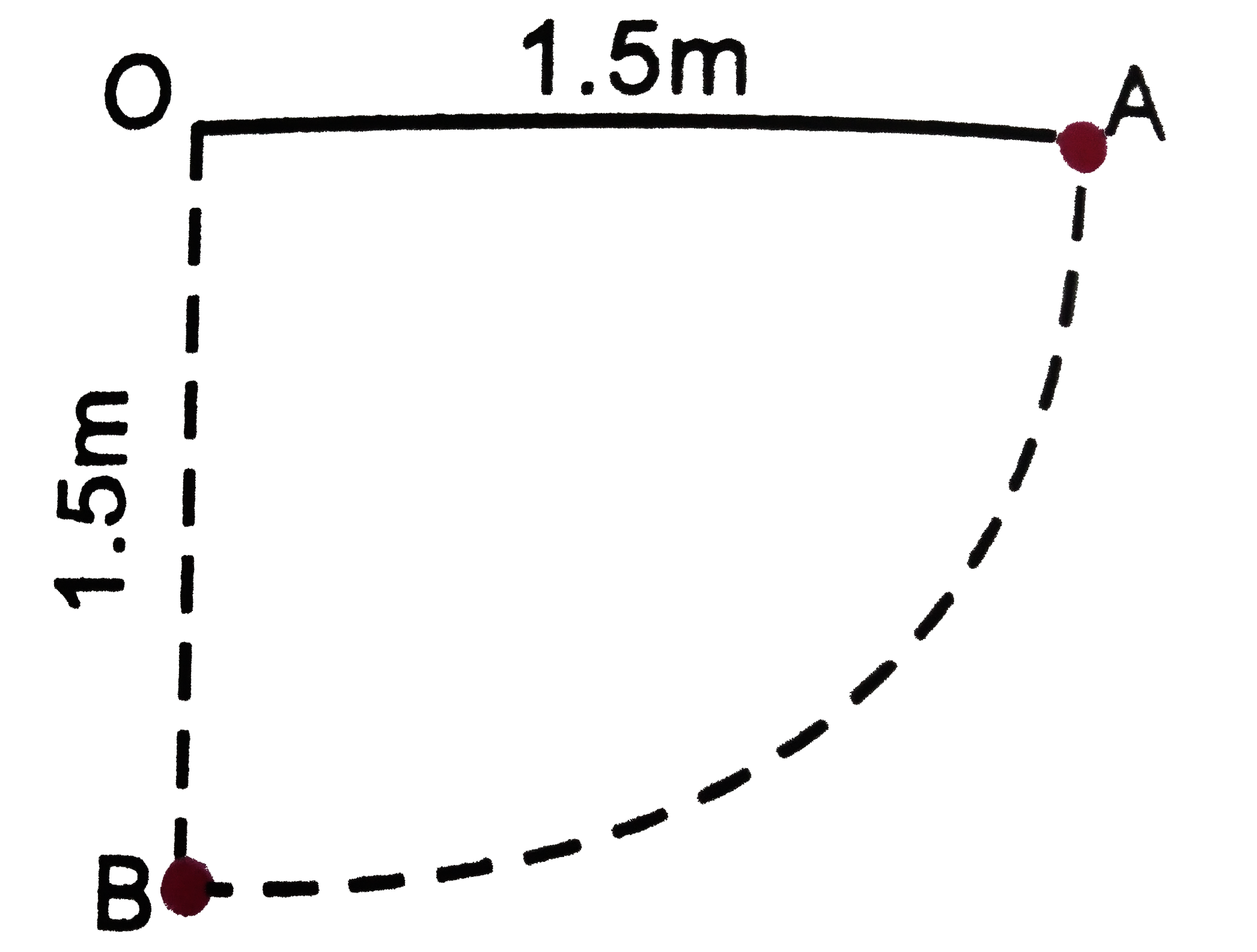 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The bob of a pendulum is released from a horizontal position. If the length of pendulum is 2 m, what is the speed with which the bob arrives at the lower most point. Assume that 10% of its energy is dissipated against air resistance.
(Take g=10ms−2)A4ms−1B6ms−1C8ms−1D10ms−1 - Question 2 - Select One
Choose the most appropriate option.
The bob of a pendulum is released from a horizontal position A as shown in the figure. If the length of the pendulumis 1.5 m, what is the speed with which the bob arrives at the lower most point B, given that it dissipated 5% of its initial energy against air resistance?
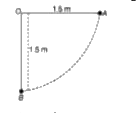 A5m/sB5.5m/sC5.3m/sD4.4m/s
A5m/sB5.5m/sC5.3m/sD4.4m/s - Question 3 - Select One
A pendulum of length 2 m lift at P . When it reaches Q , it losses 10% of its total energy due to air resistance. The velocity at Q is
 A6 m/secB1 m/ secC2 m/secD8 m/sec
A6 m/secB1 m/ secC2 m/secD8 m/sec
A simple pendulum is released from A as shown. If m and 1 represent the mass of the bob and length of the pendulum, the gain kinetic energy at B is
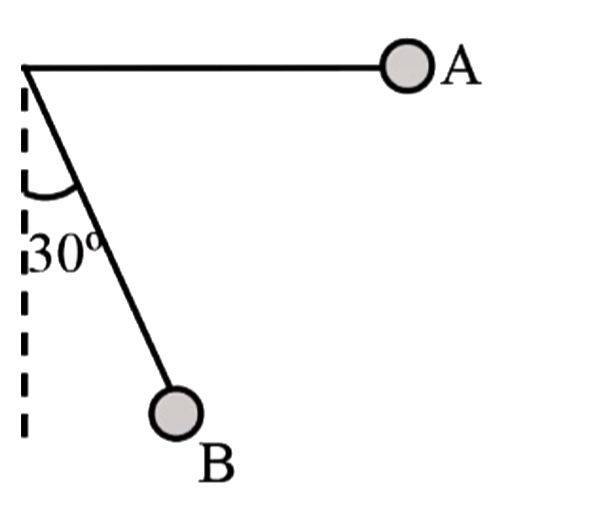 View Solution
View SolutionThe bob of a pendulum at rest is given a sharp hit to impat a horizontal velocity √10gl where l is the length of the pendulum. Find the tension in the string when a. the string is horizontal. B. The bob is at its highest point and c. the string makes an angle of 600 with teh upward vertical.
View SolutionThe string of a pendulum is 2.0m long. The bob is pulled sideways so that the string becomes horizontal and then the bob is released. What is the speed with which the bob arrives at the lowest point ? Assume theat 10% of initial energy is dissipated against air resistance. Take g=10m/s2
View SolutionThe bob of a pendulum is released from a horizontal position. If the length of pendulum is 2 m, what is the speed with which the bob arrives at the lower most point. Assume that 10% of its energy is dissipated against air resistance.
(Take g=10ms−2)View SolutionA pendulum bob on a 2 m string is displaced 60∘ from the vertical and then released. What is the speed of the bob as it passes through the lowest point in its path
View Solution

