Let the median and the mean deviation about the median of 7 observation 170, 125, 230, 190, 210, a, b be 170 and respectively. Then the mean deviation about the mean of these 7 observations is :
31
28
30
32
The correct Answer is:C
To solve the problem step by step, we will follow the given information about the observations, median, and mean deviation.
Step 1: Understanding the Observations
We are given 7 observations: 170, 125, 230, 190, 210, a, b. We need to find the values of a and b based on the median and mean deviation.
Step 2: Finding the Median
The median of a set of observations is the middle value when they are arranged in ascending order. Given that the median is 170, we can conclude that at least one of the unknowns (a or b) must be 170, because the median is the fourth term in a sorted list of 7 numbers.
Step 3: Arranging Observations
Let's arrange the observations in ascending order. We can assume:
- a ≤ b
- The sorted order will be: a, b, 125, 170, 190, 210, 230
Step 4: Mean Deviation about the Median
The mean deviation about the median is given as 2057. The formula for mean deviation about the median is:
MD=1n∑|xi−median|
Where xi are the observations. Thus, we have:
17(|a−170|+|b−170|+|125−170|+|190−170|+|210−170|+|230−170|)=2057
Step 5: Simplifying the Equation
Now, we can simplify the equation:
|a−170|+|b−170|+|125−170|+|190−170|+|210−170|+|230−170|=205
Calculating the absolute differences:
- |125−170|=45
- |190−170|=20
- |210−170|=40
- |230−170|=60
Substituting these values into the equation gives:
|a−170|+|b−170|+45+20+40+60=205
This simplifies to:
|a−170|+|b−170|+165=205
Thus,
|a−170|+|b−170|=40
Step 6: Solving for a and b
Now we have two equations:
1. |a−170|+|b−170|=40
2. a+b=300 (from the earlier calculations)
Assuming a≤b, we can express b in terms of a:
Let a=170−x and b=170+y where x+y=40.
Substituting into the second equation:
(170−x)+(170+y)=300
This simplifies to:
340+(y−x)=300⟹y−x=−40
Now we have:
1. x+y=40
2. y−x=−40
Solving these two equations simultaneously gives:
Adding them:
2y=0⟹y=0⟹x=40
Thus, we find a=130 and b=210.
Step 7: Finding the Mean
Now we can calculate the mean of the observations:
Mean=a+b+125+170+190+210+2307=130+210+125+170+190+210+2307
Calculating the sum:
=130+210+125+170+190+210+2307=10757=153.57
Step 8: Mean Deviation about the Mean
Now we find the mean deviation about the mean:
MD=17(|130−153.57|+|210−153.57|+|125−153.57|+|170−153.57|+|190−153.57|+|210−153.57|+|230−153.57|)
Calculating each term:
=17(23.57+56.43+28.57+16.43+36.43+56.43+76.43)
Summing these values gives:
=17(298.28)≈42.61
Final Answer
Thus, the mean deviation about the mean is approximately 42.61.
We are given 7 observations: 170, 125, 230, 190, 210, a, b. We need to find the values of a and b based on the median and mean deviation.
The median of a set of observations is the middle value when they are arranged in ascending order. Given that the median is 170, we can conclude that at least one of the unknowns (a or b) must be 170, because the median is the fourth term in a sorted list of 7 numbers.
Let's arrange the observations in ascending order. We can assume:
- a ≤ b
- The sorted order will be: a, b, 125, 170, 190, 210, 230
The mean deviation about the median is given as 2057. The formula for mean deviation about the median is:
Now, we can simplify the equation:
- |125−170|=45
- |190−170|=20
- |210−170|=40
- |230−170|=60
Now we have two equations:
1. |a−170|+|b−170|=40
2. a+b=300 (from the earlier calculations)
1. x+y=40
2. y−x=−40
2y=0⟹y=0⟹x=40
Now we can calculate the mean of the observations:
Now we find the mean deviation about the mean:
Thus, the mean deviation about the mean is approximately 42.61.
Topper's Solved these Questions
Similar Questions
Find the mean deviation about the mean of the distributon .
 View Solution
View SolutionFind the mean deviation about the mean of the distributon .
 View Solution
View SolutionThe mean deviation from the mean of the set of observations -1,0,4 is
View SolutionThe mean deviation from the mean of the set of observations -1,0,4 is
View SolutionCalculate the mean deviation about mean
 View Solution
View SolutionFind the mean deviation using median:
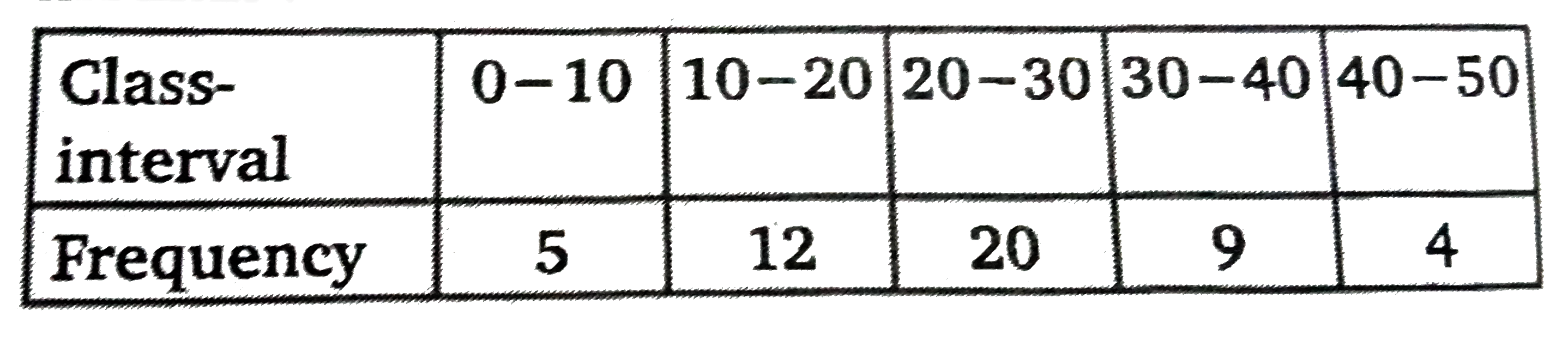 View Solution
View SolutionFind the mean deviation about the mean for the data is Question:
 View Solution
View SolutionFind the mean deviation about the mean for the data is Question:
 View Solution
View SolutionFind the mean deviation about the mean for the data in Question:
 View Solution
View SolutionFind the mean deviation about the mean for the data in Question:
 View Solution
View Solution

