If $\to a, \to b, \to c$ be three vectors such that $[\to a \to b \to c] = 4$ then $[\to a \times \to b \to b \times \to c \to c \times \to a] =$

वीडियो समाधान

उत्तर

Step by step video & image solution for If veca,vecb,vec c be three vectors such that [veca vecb vec c]=4 then [vecaxxvecb vecbxxvec c vec cxxveca]= by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS DEFAULT

समान प्रश्न

vecA+vecB+vec C=0 If so, show that, vecA×vecB=vecB×vec C=vec C×vecA
View Solution
If $\to a, \to b, \to c$ are the 3 vectors such that $| \to a | = 3, ∣ ∣ \to b ∣ ∣ = 4, | \to c | = 5, ∣ ∣ \to a + \to b + \to c ∣ ∣ = 0$ then the value of $\to a . \to b + \to b . \to c + \to c . \to a$ is :
View Solution
$\to a, \to b, \to c$ are three vectors with magnitude $| \to a | = 4, ∣ ∣ \to b ∣ ∣ = 4, | \to c | = 2$ and such that $\to a$ is perpendicular to $(\to b + \to c), \to b$ is perpendicular to $(\to c + \to a)$ and $\to c$ is perpendicualr to $(\to a + \to b)$ . It follows that $∣ ∣ \to a + \to b + \to c ∣ ∣$ is equal to :
View Solution
Let $\to a, \to b, \to c$ be three non coplanar vectors , and let $\to p, \to q and \to r$ be the vectors defined by the relation
$\to p = \frac{\to b \times \to c}{[\to a \to b \to c]}, \to q = \frac{\to c \times \to a}{[\to a \to b \to c]} and \to r = \frac{\to a \times \to b}{[\to a \to b \to c]}$
Then the value of the expension
$(\to a + \to b) . \to p + (\to b + \to c) . q + (\to c + \to a) . \to r$ is equal to
View Solution
If $\to a, \to b, \to c$ are any three noncoplanar vector, then $(\to a + \to b + \to c) [(\to a + \to b) \times (\to a + \to c)]$ is :
View Solution
Show that $\to a . (\to b \times \to c)$ is equal in magnitude to the volume of the parallelopiped formed on the three vectors, $\to a, \to b and \to c$

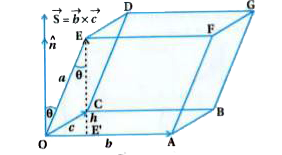
View Solution
The scalar triple product $[\to a + \to b - \to c \to b + \to c - \to a \to c + \to a - \to b]$ is equal to :
View Solution
If $\to a, \to b, \to c$ be three vectors such that $[\to a \to b \to c] = 4$ then $[\to a \times \to b \to b \times \to c \to c \times \to a]$ is equal to
View Solution

If →a,→b,→c be three vectors such that [→a→b→c]=4 then [→a×→b→b×→c→c×→a]=

समान प्रश्न

Recommended Questions

If $\to a, \to b, \to c$ be three vectors such that $[\to a \to b \to c] = 4$ then $[\to a \times \to b \to b \times \to c \to c \times \to a] =$