Two points PandQ in a plane are related if OP=OQ, where is a fixed point. This relation is :
Step by step video & image solution for Two points P and Q in a plane are related if OP = OQ, where is a fixed point. This relation is : by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RELATIONS AND FUNCTIONS BOOK - NAGEEN PRAKASHANCHAPTER - RELATIONS AND FUNCTIONS EXERCISE - Exercies 1b
18 Videos
- RELATIONS AND FUNCTIONS BOOK - NAGEEN PRAKASHANCHAPTER - RELATIONS AND FUNCTIONS EXERCISE - Exercies 1c
9 Videos
- RELATIONS AND FUNCTIONS BOOK - NAGEEN PRAKASHANCHAPTER - RELATIONS AND FUNCTIONS EXERCISE - Miscellaneous Exercise
19 Videos
- PROBABIILITYBOOK - NAGEEN PRAKASHANCHAPTER - PROBABIILITYEXERCISE - Miscellaneous Exercise
19 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - NAGEEN PRAKASHANCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Miscellaneous Exercise
23 Videos
Similar Questions
Let O be the origin. We define a relation between two points P and Q in a plane if OP=OQ. Show that the relation, so defined is an equivalence relation.
View SolutionLet O be the origin. We define a relation between two points P and Q in a plane if OP=OQ . Show that the relation, so defined is an equivalence relation.
View Solution
Knowledge Check
Two points A and B in a plane are related if OA = OB, where O is a fixed point. This relation is
Apartial order relationBequivalence relationCreflexive but not symmetricDreflexive but not transitiveA point P is moving in a plane such that the difference of its distances from two fixed points in the same plane is a constant. The path traced by the point P is a/an
ACircleBparabolaCEllipseDHyperbolaLet z1 and z2 be the roots of the equation z2+pz+q=0. Suppose z1 and z2 are represented by points A and B in the Argand plane such that ∠AOB=α, where O is the origin.
Statement-1: If OA=OB, then p2=4qcos2α2
Statement-2: If affix of a point P in the Argand plane is z, then zeia is represented by a point Q such that ∠POQ=α and OP=OQ.AStatement-1 is True, Statement-2 is True: Statement-2 is a correct exp,anation for statement-1.BStatement-1 is true, statement -2 is true, Statement-2 is not a correct explanation for statement-1.CStatement-1 is True, statement-2 is false,Dstatement-1 is False, Statement-2 is true.
A normal is drawn at a point A (x, y) of a curve. It meets the X -axis and Y - axis at point P and Q respectively such that 1OP+1OQ=1 where O is the origin. Then, the equation of such a curve passing through (5, 4) is
View SolutionIn the figure, ∠QPR=∠PQR and M and N are respectively on sides QR and PR such that QM = PN. Prove that OP=OQ, where O is the point of intersection of PM and QN.
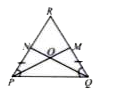
View SolutionA point moves in a plane so that its distances PA and PB from two fixed points A and B in the plane satisfy the relation PA−PB=k(k≠0), then the locus of P, is
View SolutionOn the set of all points in a plane, the relation defined by the phrase 'at the same distance from the origin' is an equivalence relation.
View SolutionLet P(-7,1,-5) be a point on a plane and let O be the origin. If OP is normal to the plane, then the equation of the plane is
View Solution
