सदिश →a=ˆi+ˆj−2ˆk के दिक्-अनुपात लिखिए
a=1,b=2 और c=−2
a=−1,b=1 और c=−2
a=1,b=1 और c=−2
a=1,b=1 और c=−1
The correct Answer is:C
माना सदिश →r=xˆi+yˆj+zˆk के दिक्-अनुपात a,b,c सदिश के क्रमागत घटक x,y,z होते हैं। इसलिए a=1,b=1 और c=−2 है। पुनः यदि l,m और n दिए हुए सदिश के दिक्-कोसाइन हैं तो
|→r|=√(1)2+(1)2+(−2)2
=√1+1+4
√6
अब l=a|→r|=1√6,m=b|→r|=1√6,n=c|→r|=−2√6
अतः दिक्-कोसाइन =(1√6,1√6,−2√6)
Topper's Solved these Questions
- सदिश बीजगणित BOOK - MANOHAR RAYCHAPTER - सदिश बीजगणित EXERCISE - प्रश्नावली 10(A)
9 Videos
- सदिश बीजगणित BOOK - MANOHAR RAYCHAPTER - सदिश बीजगणित EXERCISE - प्रश्नावली 10 (A)
1 Videos
- सततता तथा अवकलनीयता BOOK - MANOHAR RAYCHAPTER - सततता तथा अवकलनीयता EXERCISE - इंजीनियरिंग परीक्षाओ के प्रश्न
7 Videos
- समाकलनBOOK - MANOHAR RAYCHAPTER - समाकलनEXERCISE - प्रश्नावली 7(Z)
40 Videos
Similar Questions
(i) पश्चिम से 50∘ दक्षिण में 20 किमी के विस्थापन का आलेखीय निरूपण कीजिए।
(ii) उत्तर से 30∘ पूर्व में 40km के विस्थापन का आलेखीय निरूपण कीजिए।
View Solutionदी गई आकृति में निम्न सदिशों को पहचानिए-
(i) सह-आदिम (ii) समान (iii) संरेख परन्तु असमान
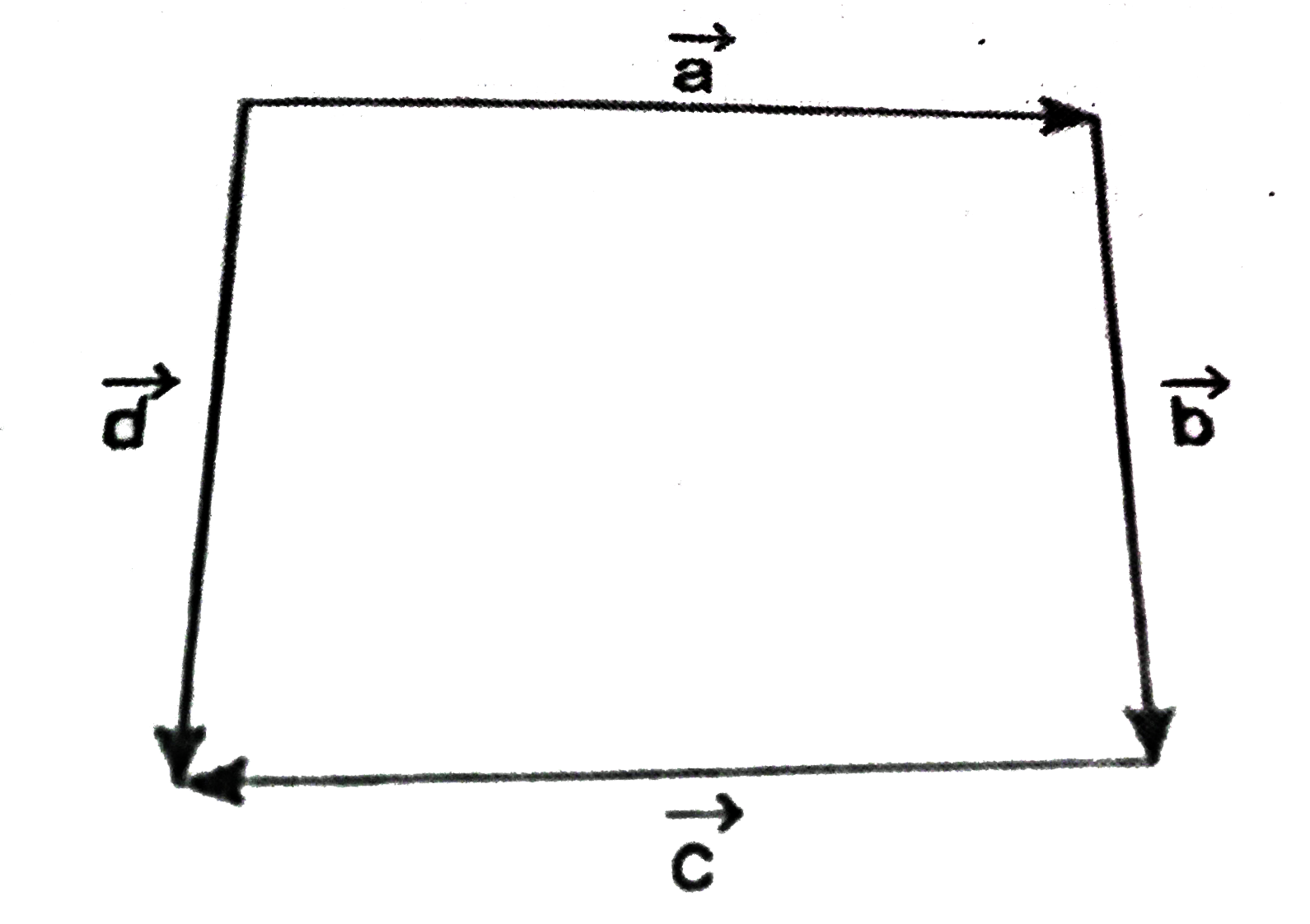
View Solutionlimx→0sin(πcos2x)x2 का मान है ।
View Solution∫x0dx का मान होगा
View SolutionIf vecA=hati+2hatk and vecB=hatj-hatk then vecAxxvecB=
View SolutionIf →a=2ˆi+ˆj+ˆk,→b=ˆi+2ˆj+2ˆk,→c=ˆi+ˆj+2ˆkand[→a→b→i]ˆi+[→a→b→j]ˆj+[→a→bˆk]k is equal to
View Solutionयदि →a=ˆi−ˆj और →b=−ˆj+2ˆk हो, तो (→a−2→b).(→a+→b) का मान ज्ञात कीजिए ।
View Solution→a×→b का मान ज्ञात कीजिए जबकि :
→a=ˆi−2ˆj+2ˆk,→b=3ˆi+ˆj−2ˆk
View Solutionसदिश 3ˆi−2ˆj+6ˆk की दिक्-कोज्याएँ .......... है
View SolutionLet →a be a unit vector coplanar with ˆi−ˆj+2ˆk and 2ˆi−ˆj+ˆk such that →a is perpendicular to ˆi−2ˆj+ˆk. If the projecton of →a along ˆi−ˆj+2ˆk is λ, then the value of 1λ2 is equal to
View Solutionसदिश 4ˆi−ˆj+3ˆk तथा −2ˆi+ˆj−2ˆk के लम्बवत 9 इकाई परिमाण वाला सदिश ज्ञात किजिए।
View Solutionसदिश →a=ˆi+2ˆj−3ˆk तथा →b=3ˆi−ˆj+2ˆk दोनो के लम्बवत एक एसा सदिश ज्ञात किजिए, जिसका परिमाण √171 हो।
View SolutionIf →a=2ˆi−ˆj+2ˆk,→b=ˆi+ˆj+2ˆk,→c=3ˆi−ˆj+ˆk Find (→a×→b)→cand→a(→b×→c) Are they equal?
View SolutionLet →a=ˆi−ˆj+ˆk,→b=2ˆi+ˆj+ˆkand→c=ˆi+ˆj−2ˆk, then the value of [→a→b→c] is equal to
View Solution→a=ˆi+2ˆj+2ˆk এবং →b=ˆj+2ˆk হলে →a ভেক্টরের ওপর →b ভেক্টরের স্কেলার ও ভেক্টর অভিক্ষেপ নির্ণয় করো।
View Solution
