ABCD समान्तर चतुर्भुज के विकर्ण P पर मिलते है O कोई बिंदु है। सिद्ध करो कि सदिश
−−→OA+−−→OB+−−→OC+−−→OD=4−−→OP

−−→OA+−−→OC=2−−→OP……………….i
और −−→OB+−−→OD=2−−→OP……………ii
सभी i और ii जोड़ने पर
−−→OA+−−→OB+−−→OC+−−→OD=2−−→OP+2−−→OP
=4−−→OP
इसे इस प्रकार भी लिख सकते हैं।
ABCD समान्तर चतुर्भज के विकर्णों का प्रतिच्छेद बिंदु P है। सिद्ध करो कि किसी मूलबिंदु के लिए शीर्षों के स्थिति सदिशों का योग P के स्थिति सदिश का चार गुना होता है।
Topper's Solved these Questions
- सदिश बीजगणित BOOK - MANOHAR RAYCHAPTER - सदिश बीजगणित EXERCISE - प्रश्नावली 10(A)
9 Videos
- सदिश बीजगणित BOOK - MANOHAR RAYCHAPTER - सदिश बीजगणित EXERCISE - प्रश्नावली 10 (A)
1 Videos
- सततता तथा अवकलनीयता BOOK - MANOHAR RAYCHAPTER - सततता तथा अवकलनीयता EXERCISE - इंजीनियरिंग परीक्षाओ के प्रश्न
7 Videos
- समाकलनBOOK - MANOHAR RAYCHAPTER - समाकलनEXERCISE - प्रश्नावली 7(Z)
40 Videos
Similar Questions
(i) पश्चिम से 50∘ दक्षिण में 20 किमी के विस्थापन का आलेखीय निरूपण कीजिए।
(ii) उत्तर से 30∘ पूर्व में 40km के विस्थापन का आलेखीय निरूपण कीजिए।
View Solutionदी गई आकृति में निम्न सदिशों को पहचानिए-
(i) सह-आदिम (ii) समान (iii) संरेख परन्तु असमान
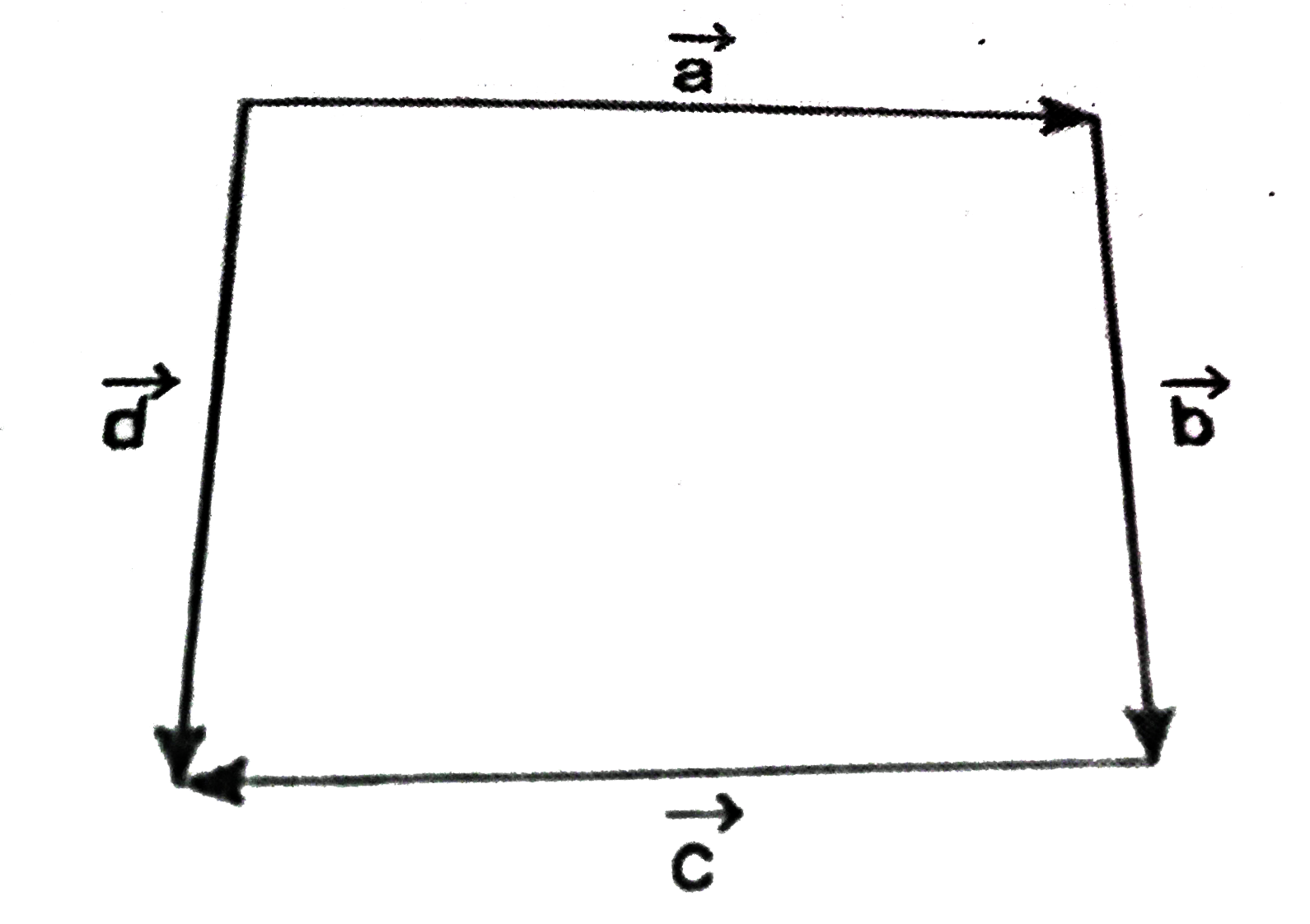
View Solutionlimx→0sin(πcos2x)x2 का मान है ।
View Solution∫x0dx का मान होगा
View SolutionABCD is parallelogram and P is the point of intersection of its diagonals. If O is the origin of reference, show that →OA+→OB+→OC+→OD=4→OP.
View SolutionLet ABCD be a p[arallelogram whose diagonals intersect at P and let O be the origin. Then prove that →OA+→OB+→OC+→OD=4→OP.
View SolutionIf ABCD is a rhombus whose diagonals cut at the origin O, then proved that →OA+→OB+→OC+→OD+→O.
View SolutionIf O is the circumcentre and P the orthocentre ( of Delta ABC, prove that )/(OA)+vec OB+vec OC=vec OP
View SolutionGiven a regular hexagon ABCDEF with centre o,show that vec OB-vec OA=vec OC-vec OD
View SolutionABCD एक समान्तर चतुर्भुज के विकर्ण P पर मिलते है, O कोई बिन्दु है। सिद्ध करो कि सदिश −−→OA+−−→OB+−−→OC+−−→OD=4−−→OP
View Solutionमाना कि O समष्टभुज ABCDEF का केंद्र हैं, तो
−−→OA+−−→OB+−−→OC=−−→OD+−−→OE+−−→OF.
View Solutionमान लीजिये की ABCD एक समान्तर चतुर्भुज है जिसके विकर्ण P पर प्रतिछेद करते है तथा मान लीजिये की O मूलबिंदु है, तो −−→OA+−−→OB+−−→OC+−−→OD किसके बराबर है?
View SolutionABCDE एक समपंचभुज है। O इसका केंद्र है। सिद्ध कीजिए कि −−→OA+−−→OB+−−→OC+−−→OD+−−→OE=→0
View SolutionABCD समान्तर चतुर्भुज है तथा P इसके विकर्ण का प्रतिच्छेद बिन्दु है | यदि O मूल बिन्दु है, तो प्रदर्शित कीजिए कि −−→OA+−−→OB+−−→OC+−−→OD=4−−→OP होगा |
View SolutionIf E is the intersection point of diagonals of parallelogram ABCD and −−→OA+−−→OB+−−→OC+−−→OD=x−−→OE where O is origin then x=
View Solution
