सदिश विधि द्वारा सिद्ध कीजिए कि
(i) (→a+→b)2+→a2+2→a.→b+→b2 (ii) (→a−→b)2=→a2−2→a.→b+→b2
(iii)(→a+→b).(→a−→b)=→a2−→b2 (iv) →a.(→b−→c)=→a.→b−→a.→c
(i)माना →a=a1ˆi+a2ˆj+a3ˆk
→b=b1ˆi+b2ˆj+b3ˆk
∴ बायां पक्ष =(→a+→b)2
=[(a1ˆi+a2ˆj+a3ˆk)+(b1ˆi+b2ˆj+b3ˆk)]2
(a1ˆi+a2ˆj+a3ˆk)2+(b1ˆi+a2ˆj+a)3ˆk).(b1ˆi+b2ˆj+b3ˆk)
[∵→a2=a21+a22+a23,→b2=b21+b22+b23]
=(a21+a22+a23)+(b21+b22+b23)+2(a1b1+b1b2+a3b3)
=→a2+→b2+2→a.→b
→a2+2→a.→b+→b2
(ii) (→a−→b)2=→a2−2→a.→b+→b2
बायां पक्ष =(→a−→b)2
=[(→a1ˆi+a2ˆj+a3ˆk)−(b1ˆi+b2ˆj+b3ˆk)]2
=(a1ˆi+a2ˆj+a3ˆk)2+(b1ˆi+b2ˆj+b3ˆk)2
−2(a1ˆi+a2ˆj+a3ˆk).(b1ˆi+b2ˆj+b3ˆk)
=(a21+a22+a23)+(b21+b22+b23)−2(a1b1+a2b2+a3b3)
=→a2−2→a.→b+→b2
(iii) (→a+→b).(→a−→b)=→a2−→b2
बायां पक्ष =(→a+→a−→b)
={(a1ˆi+a2ˆj+a3ˆk)+(b1ˆi+b2ˆk)}.{(a1ˆi+a2ˆj+a3ˆk−b1ˆi−b2ˆj−b3ˆk)}
=(a1+b1)ˆi+(a2+b2)ˆj+(a3+b3)ˆk}.{(a1−b1ˆi+(a∘−b2)ˆj+(a3−b3)ˆk}
=(a1+b1)(a1−b1)+(a2+b2)(a2−b2)+(a3+b3)(a3−b3)
=→a2−→b2
(iv) →a.(→b−→c)=→a.→b−→a.→c
माना →a=a1ˆi+a2ˆj+a3ˆk
→b=b1ˆi+b2ˆj+b3ˆk
→c=c1ˆi+c2ˆj+c3ˆk
बायां पक्ष →a.(→b−→c)
=(a1ˆi+a2ˆj+a3ˆk).[(b1ˆi+b2ˆj+b3ˆk)−(c1ˆi+c2ˆj+c3ˆk)]
=(a1ˆi+a2ˆj+a3ˆk).[(b1−c1)ˆi+(b2−c2)ˆj+(b3−c3)ˆk]
=a1(b1−c1)+a2(b2−c2)+a3(b3−c3)
=a1b1−a1c1+a2b2−a2c2+a2b2+a3C3
=a1b1+a2b2+a3b3−(a1c1+a2c2+a3c3)
=→a.→b−→a.→c
Topper's Solved these Questions
- सदिश बीजगणित BOOK - MANOHAR RAYCHAPTER - सदिश बीजगणित EXERCISE - प्रश्नावली 10(A)
9 Videos
- सदिश बीजगणित BOOK - MANOHAR RAYCHAPTER - सदिश बीजगणित EXERCISE - प्रश्नावली 10 (A)
1 Videos
- सततता तथा अवकलनीयता BOOK - MANOHAR RAYCHAPTER - सततता तथा अवकलनीयता EXERCISE - इंजीनियरिंग परीक्षाओ के प्रश्न
7 Videos
- समाकलनBOOK - MANOHAR RAYCHAPTER - समाकलनEXERCISE - प्रश्नावली 7(Z)
40 Videos
Similar Questions
(i) पश्चिम से 50∘ दक्षिण में 20 किमी के विस्थापन का आलेखीय निरूपण कीजिए।
(ii) उत्तर से 30∘ पूर्व में 40km के विस्थापन का आलेखीय निरूपण कीजिए।
View Solutionदी गई आकृति में निम्न सदिशों को पहचानिए-
(i) सह-आदिम (ii) समान (iii) संरेख परन्तु असमान
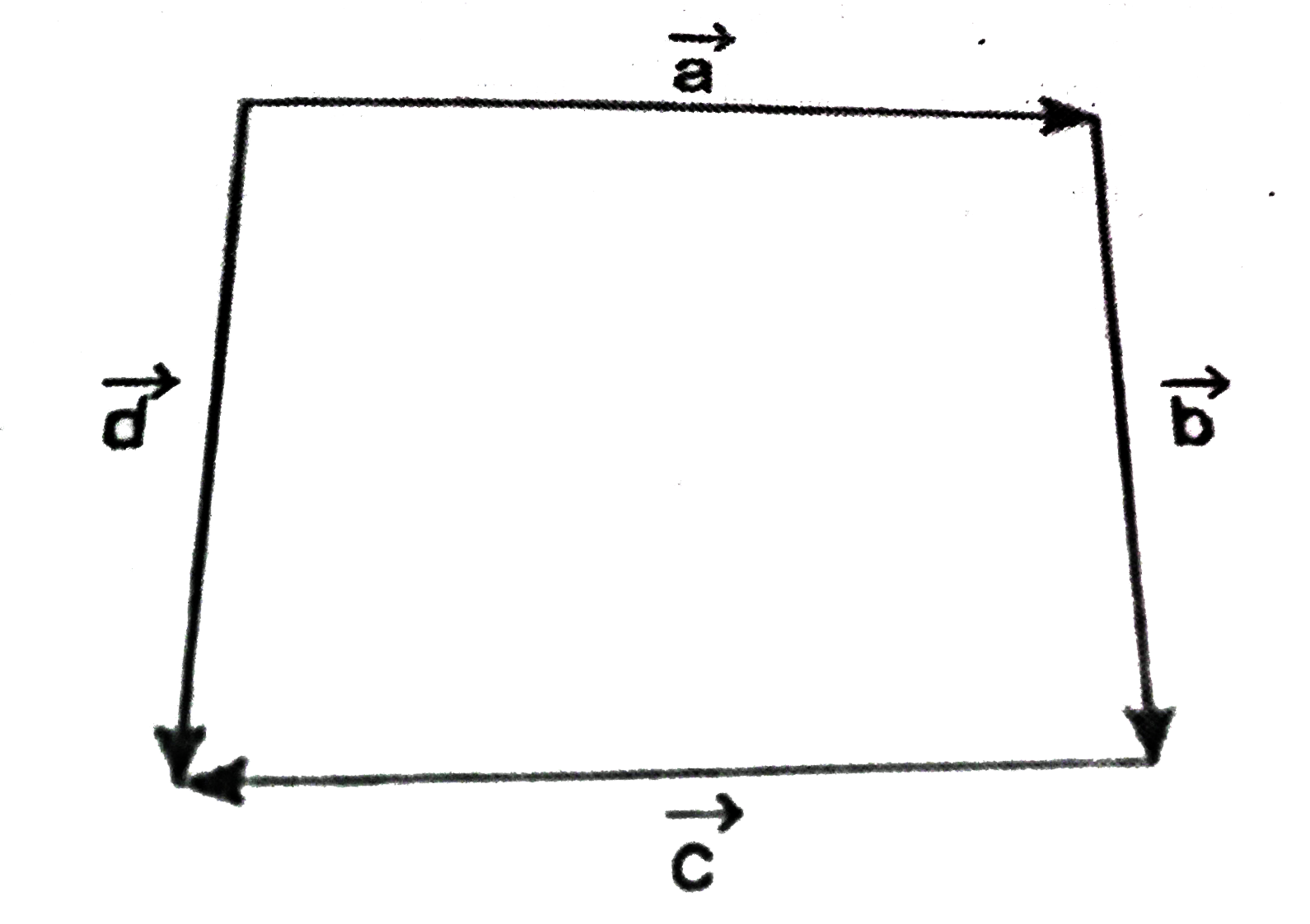
View Solutionlimx→0sin(πcos2x)x2 का मान है ।
View Solution∫x0dx का मान होगा
View Solution∣∣→a±→b∣∣2=|→a|2+∣∣→b∣∣2±2|→a|∣∣→b∣∣cosθ and (→a+→b).(→a−→b)=|→a|2−∣∣→b∣∣2
View SolutionIf→a,→b,→c are three mutually perpendicular vectors, then the vector which is equally inclined to these vectors is (A) →a+→b+→c (B) →a|→a|+→b∣∣→b∣∣+→/|→c| (C) →a|→a|2+→b∣∣→b∣∣2+→c|→c|2 (D) |→a|→a−∣∣→b∣∣→b+|→c|→c
View SolutionProve that ∣∣→a×→b∣∣2=∣∣∣→a⋅→a→a⋅→b→a⋅→b→b⋅→b∣∣∣.
View SolutionLet →a,→b,→c be three vectors such that
→a⊥(→b+→c),→b⊥(→c+→a)and→c⊥(→a+→b), if |→a|=1,∣∣→b∣∣=2,
|→c|=3, then ∣∣→a+→b+→c∣∣ is,
View Solutionसदिशों तथा के लिए सिद्ध कीजिए कि
∣∣→a×→b∣∣2=∣∣∣→a.→a→a.→b→a.→b→a.→b∣∣∣
View Solutionसिद्ध कीजिए :
(i) (→A+→B)−(→A−→B)2=4(→A⋅→B).
(ii) (→A+→B)×(→A−→B)=−2(→A×→B).
(iii) (→A×→B)2+(→A⋅→B)2=A2B2.
View Solutionसिद्ध करें कि
(i) [→a+→b →b+→c →c+→a]=2[→a →b →c]
(ii) →a+→b,→b+→c और →c+→a असमतलीय होगें यदि →a,→b,→c तीन असमतलीय सदिश हों ।
View SolutionShow that (→a×→b)2=|→a|2∣∣→b∣∣2−(→a.→b)2=∣∣∣→a.→a→a.→b→a.→b→b.→b∣∣∣
View SolutionIf →a,→b,→c are unit vectors, then :
∣∣→a−→b∣∣2+∣∣→b−→c∣∣2+|→c−→a|2 does not exceed :
View SolutionIf→a,→b,→c are three mutually perpendicular vectors, then the vector which is equally inclined to these vectors is (A) →a+→b+→c (B) →a|→a|+→b∣∣→b∣∣+→/|→c| (C) →a|→a|2+→b∣∣→b∣∣2+→c|→c|2 (D) |→a|→a−∣∣→b∣∣→b+|→c|→c
View Solutionसिद्ध करो कि (→a→a2−→b→b2)2=⎛⎜⎝→a−→b|→a|∣∣→b∣∣⎞⎟⎠2
View Solution
