तीन सदिश →a,→b और →c प्रतिबंध →a+→b+→c=→0 को संतुष्ट करते हैं। यदि |→a|=1,∣∣→b∣∣ और |→c|=2 तो राशि μ=→a.→b+→b.→c+→c.→a का मान ज्ञात कीजिए।
∵→a+→b+→c=0 इसलिए
→a.(→a+→b+→c)=0
या →a,→a+→a.→b+→a.→c=0
या →a.→b+→a.→c=−|→a|2=−1…………….i
पुनः →b.(→a+→b+→c)=0
या →a.→b+→b.→c=−∣∣→b∣∣2=−16………………i
इसी प्रकार
समीकरण i,ii iii को जोड़ने पर
2(→a.→b+→b.→c+→a.→c)=−21
या 2μ=−21
या μ=−212
Topper's Solved these Questions
- सदिश बीजगणित BOOK - MANOHAR RAYCHAPTER - सदिश बीजगणित EXERCISE - प्रश्नावली 10(A)
9 Videos
- सदिश बीजगणित BOOK - MANOHAR RAYCHAPTER - सदिश बीजगणित EXERCISE - प्रश्नावली 10 (A)
1 Videos
- सततता तथा अवकलनीयता BOOK - MANOHAR RAYCHAPTER - सततता तथा अवकलनीयता EXERCISE - इंजीनियरिंग परीक्षाओ के प्रश्न
7 Videos
- समाकलनBOOK - MANOHAR RAYCHAPTER - समाकलनEXERCISE - प्रश्नावली 7(Z)
40 Videos
Similar Questions
(i) पश्चिम से 50∘ दक्षिण में 20 किमी के विस्थापन का आलेखीय निरूपण कीजिए।
(ii) उत्तर से 30∘ पूर्व में 40km के विस्थापन का आलेखीय निरूपण कीजिए।
View Solutionदी गई आकृति में निम्न सदिशों को पहचानिए-
(i) सह-आदिम (ii) समान (iii) संरेख परन्तु असमान
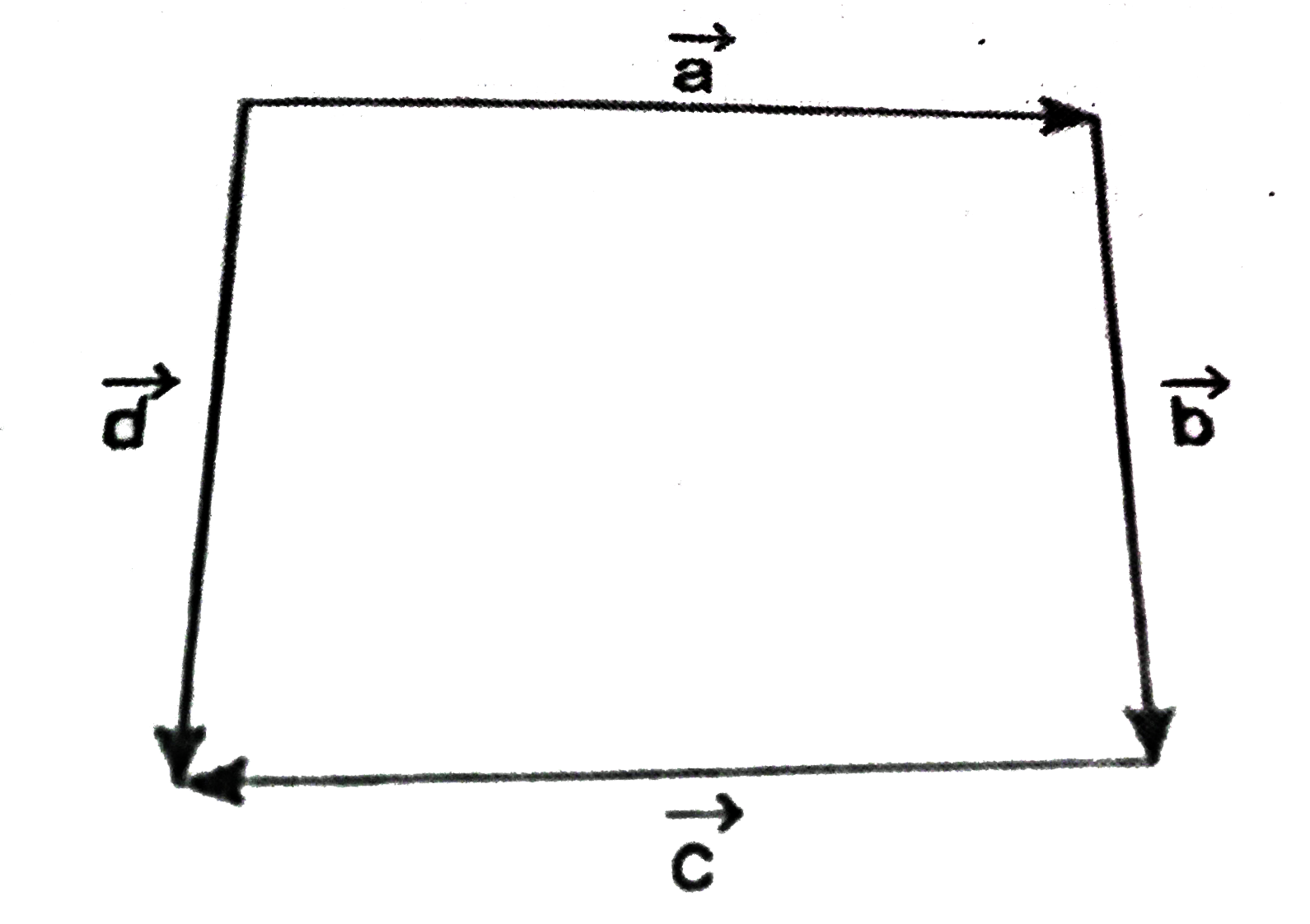
View Solutionlimx→0sin(πcos2x)x2 का मान है ।
View Solution∫x0dx का मान होगा
View SolutionConsider vectors →a,→b,→c,→p=(→b.→c)→a−(→c.→a)→b,→q=(→a.→c)→b−(→a.→b)→c,→r=(→b.→a)→c−(→b.→c)→a, then
View Solutionतीन सदिश →a,→b और →c प्रतिबंध →a+→b+→c=→0 को संतुष्ट करते है! यदि |→a|=3,∣∣→b∣∣=4 और |→c|=2 तो राशि μ=→a.→b+→b.→c+→c.→a का मान ज्ञात कीजिए!
View SolutionIf |→a|=5,∣∣→b∣∣=6,|→c|=7 and →a+→b+→c=→0, find →a.→b+→b.→c+→c.→a.
View SolutionIf |→a|=3,∣∣→b∣∣=1,|→c|=4 and →a+→b+→c=→0, find the value of →a.→b+→b+→c.→c+→c.→a.
View Solutionयदि →a,→b,→c मात्रक सदिश इस प्रकार है कि →a+→b+→c=→0 तो →a.→b+→b.→c+→c.→a का मान ज्ञात कीजिए।
View Solutionতিনটি ভেক্টর →a,→b,→c এমন যে, →a+→b+→c=→0, যদি |→a|=1,∣∣→b∣∣=4 ও |→c|=2 হয় তবে μ=→a.→b+→b.→c+→c.→a রাশির মান নির্ণয় করাে।
View Solution|→a|=5,∣∣→b∣∣=6,|→c|=7 மற்றும்→a+→b+→c=→0 எனில், →a.→b+→b.→c+→c.→a ஐக் காண்க.
View SolutionIf →a,→b,→c are unit vectors such that →a+→b+→c = →0, find the value of →a.→b+→b.→c+→c.→a.
View SolutionThree vectors →a,→b,and→c satisfy the condition→a+→b+→c=→0. Evaluate the quantity μ=→a.→b+→b.→c+→c.→a. If |→a|=1,∣∣→b∣∣=4 and |→c|=2.
View SolutionIf |→a|=3,∣∣→b∣∣=1,|→c|=4 and →a+→b+→c=→0, find the value of →a.→b+→b.→c+→c.→a.
View SolutionIf →a,→b,→c are three vectors such that
→a+→b+→c=→0,|→a|=1∣∣→b∣∣=2,|→c|=3 , then
→a.→b+→b.→c+→c.→a is equal to
View Solution
