यदि सदिश →a और →b के लिए ∣∣→a+→b∣∣=√29 और →a×(2ˆi+3ˆj+4ˆk)=(2ˆi+3ˆj+4ˆk)×→b है तब (→a+→b).(−7ˆi+2ˆj+3ˆk) का एक सम्भावित मान ज्ञात कीजिए।
→a×(2ˆi+3ˆj+4ˆk)=(2ˆi+3ˆj+4ˆk)×→b
∴→a×(2ˆi+3ˆj+4ˆk)=−→b×(2ˆi+3ˆj+4ˆk)[→a×→b=−→b×→a]
→a×(2ˆi+3ˆj+4ˆk)+→b(2ˆi+3ˆj+4ˆk)=0
(2ˆi+3ˆj+4ˆkj)×(→a+→b)=0
→a+→b=λ(2ˆi=3ˆj+4ˆk)
√29=±λ√(2)2+(3)2+(4)2
√29=±λ(2+9+16)
√29=±λ√29
λ=±1⇒→a+→b(2ˆi+3ˆj+4ˆk)
अब (→a+→b).(−7ˆi+2ˆj+3ˆk)=±(2ˆi+3ˆj+4ˆk).(−7ˆi+3ˆj+4ˆk)
=±(−14+6+12)
=±4
Topper's Solved these Questions
- सदिश बीजगणित BOOK - MANOHAR RAYCHAPTER - सदिश बीजगणित EXERCISE - प्रश्नावली 10(A)
9 Videos
- सदिश बीजगणित BOOK - MANOHAR RAYCHAPTER - सदिश बीजगणित EXERCISE - प्रश्नावली 10 (A)
1 Videos
- सततता तथा अवकलनीयता BOOK - MANOHAR RAYCHAPTER - सततता तथा अवकलनीयता EXERCISE - इंजीनियरिंग परीक्षाओ के प्रश्न
7 Videos
- समाकलनBOOK - MANOHAR RAYCHAPTER - समाकलनEXERCISE - प्रश्नावली 7(Z)
40 Videos
Similar Questions
(i) पश्चिम से 50∘ दक्षिण में 20 किमी के विस्थापन का आलेखीय निरूपण कीजिए।
(ii) उत्तर से 30∘ पूर्व में 40km के विस्थापन का आलेखीय निरूपण कीजिए।
View Solutionदी गई आकृति में निम्न सदिशों को पहचानिए-
(i) सह-आदिम (ii) समान (iii) संरेख परन्तु असमान
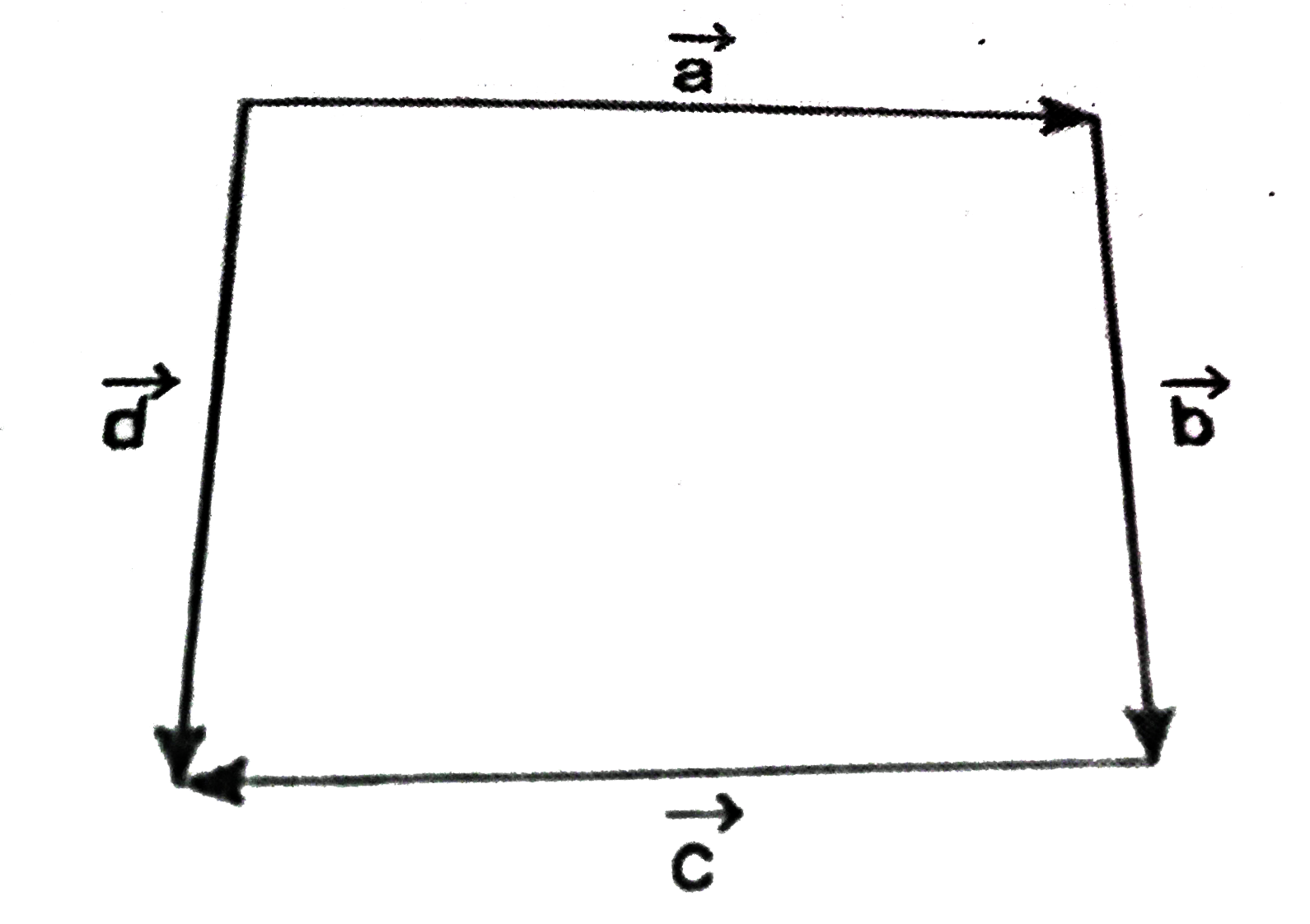
View Solutionlimx→0sin(πcos2x)x2 का मान है ।
View Solution∫x0dx का मान होगा
View SolutionIf →a=7ˆi+3ˆj−6ˆk, →b=2ˆi+5ˆj−ˆk and →c=−ˆi+2ˆj+4ˆk. Find (→a−→b)×(→c−→b).
View SolutionIf →aand→b are vectors such that ∣∣→a+→b∣∣=√29and→a×(2ˆi+3ˆj+4ˆk)=(2ˆi+3ˆj+4ˆk)×→b, then possible value of (→a+→b).(−7ˆi+2ˆj+3ˆk) is (A) 0 (B) 3 (C) 4 (D) 8
View Solutionदर्शाइए कि सदिश →a=ˆi−2ˆj+3ˆk,→b=−2ˆi+3ˆj−4ˆk और →c=ˆi−3ˆj+5ˆkसमतलीय है l
View Solutionयदि →A=−2ˆi+3ˆj+ˆk तथा →B=ˆi+2ˆj−4ˆk हों,तो →A व →B के बीच कोण ज्ञात कीजिए |
View Solutionयदि →a और →b असंरेख है ,तो x का मान ज्ञात कीजिए| जिसके लिए सदिश α=(2x+1)→a−→b और β=(x−2)→a+→b संरेख है
View Solutionयदि →a=2ˆi−3ˆj+6ˆk,→b=2ˆi+ˆj−4ˆk हो, तो सिद्ध कीजिए कि
(→a+→b).(→a−→b)=|→a|2−∣∣→b∣∣2.
View Solutionयदि →a=λˆi+2ˆj+2ˆk तथा→b=2ˆi+2ˆj+λˆk समकोण पर है , तब ∣∣→a+→b∣∣=∣∣→a−→b∣∣ का मान -
View SolutionIf →a=2ˆi−3ˆj+4ˆk,→a.→b=2 and →a×→b=ˆi+2ˆj+ˆk, then →b is equal to
View Solutionयदि →a=2ˆi+5ˆj+3ˆk,→b=3ˆi+3ˆj+6ˆk और →c=2ˆi+7ˆj+4ˆk, तो (→a−→b)×(→c−→a) का मान ज्ञात कीजिए।
View Solutionयदि →a=ˆi+ˆj+ˆk,→a⋅→b=2 और →a×→b=2ˆi+ˆj−3ˆk है, तो →b है:
View SolutionIf →aand→b are vectors such that |→a+ecb|=√29and→a×(2ˆi+3ˆj+4ˆk)=(2ˆi+3ˆj+4ˆk)×→b, then possible value of (→a+→b).(−7ˆi+2ˆj+3ˆk) is (A) 0 (B) 3 (C) 4 (D) 8
View Solution
