I धारावाही, N फेरों ओर R त्रिज्या वाली वृत्ताकार कुंडली के लिए, इसके अक्ष पर, केन्द्र से x दूरी पर स्थित किसी बिंदु पर चुंबकीय क्षेत्र के लिए निम्न व्यंजक है :
B=μ0IR2N2(x2+R2)3/2
(a) स्पष्ट कीजिए, इससे कुंडली के केंद्र पर चुंबकीय क्षेत्र के लिए सुपरिचित परिणाम, कैसे प्राप्त किया जा सकता है?
(b) बराबर त्रिज्या R, एवं फेरों की संख्या N वाली दो वृत्ताकार कुंडलियाँ एक-दूसरे से R दूरी पर एक-दूसरे के समांतर, अक्ष मिलाकर रखी गई है। दोनों में समान विघुत धारा एक ही दिशा में प्रवाहित हो रही है। दर्शाइए की कुंडलियों के अक्ष के लगभग मध्यबिंदु पर क्षेत्र, एक बहुत छोटी दूरी के लिए जोकि R से कम है, एकसमान है और इस क्षेत्र का लगभग मान निम्न है :
B=0.72μ0NIR
[बहुत छोटे-से-क्षेत्र पर एकसमान चुंबकीय क्षेत्र उत्पन्न करने के लिए बनायी गई ऊपर वर्णित व्यवस्था हेल्महोल्ट्ज कुंडलियों के नाम से जानी जाती है।]
(a) कुण्डली के केन्द्र पर चुम्बकीय क्षेत्र के लिए x = 0
B=μ0iR2N2R3=μ0Ni2R
(b) चुम्बकीय क्षेत्र के परिवर्तन की दर = dBdx
एकसमान चुम्बकीय क्षेत्र के लिये dBdx = नियत
∴d2Bdx2=0
एक कुण्डली के कारण चुम्बकीय क्षेत्र B=μ0NiR22(a2+x2)3/2
∴dBdx=μ0NiR22ddx(R2+x2)−3/2
=μ0NiR22(−32)(R2+x2)−5/22x
=−32μ0NiR2(R2+x2)−5/2x
d2Bdx2=−32μ0NiR2ddx[x(R2+x2)−5/2]
=−32μ0NiR2[(R2+x2)−5/2+x(−52)(R2+x2)−7/22x]
=−32μ0NiR2[(R2+x2)−5/2−5x2(R2+x2)−7/2]
=−32μ0NiR2(R2+x2)−7/2[(R2+x2)−5x2]
यदि d2Bdx2=0, तब (R2+x2)−5x2=0
अथवा 4x2=R2 अथवा x=±R2
इस प्रकार, कुण्डली के केन्द्र से दोनों ओर R2 दूरी पर चुम्बकीय क्षेत्र दूरी बढ़ने पर एकसमान रूप से घटता है। अतः दोनों कुण्डलियों के बीच चुम्बकीय क्षेत्र R2 दूरी पर एकसमान है। वहाँ पर दोनों कुण्डलियों के कारण चुम्बकीय क्षेत्र
B=2×μ0NiR22(R2+R24)3/2
=8(5)3/2μ0NiR=0.77μ0NiR
यदि परिणाम हैल्महोल्ट्ज स्पर्शज्या धारामापी में प्रयुक्त किया जाता है।
Topper's Solved these Questions
- चल कुण्डली धारामापी BOOK - NOOTAN HINDICHAPTER - चल कुण्डली धारामापी EXERCISE - वस्तुनिष्ठ प्रश्न
29 Videos
- चल कुण्डली धारामापी BOOK - NOOTAN HINDICHAPTER - चल कुण्डली धारामापी EXERCISE - अतिलघु उत्तरीय
23 Videos
- चल कुण्डली धारामापी BOOK - NOOTAN HINDICHAPTER - चल कुण्डली धारामापी EXERCISE - एन.सी.ई.आर.टी. प्रश्न
13 Videos
- गतिमान आवेश तथा चुंबकीय क्षेत्र BOOK - NOOTAN HINDICHAPTER - गतिमान आवेश तथा चुंबकीय क्षेत्र EXERCISE - वस्तुनिष्ठ प्रकार प्रश्न
39 Videos
- तरंग प्रकाशिकी तथा हाइगेन्स का सिद्धांतBOOK - NOOTAN HINDICHAPTER - तरंग प्रकाशिकी तथा हाइगेन्स का सिद्धांतEXERCISE - वस्तुनिष्ट प्रकार प्रश्न ( एकल उत्तर प्रकार )
1 Videos
Similar Questions
एक वृत्ताकार लूप का पृष्ठ क्षेत्रफल A तथा इसमें प्रवाहित धारा i है। चुम्बकीय क्षेत्र की तीव्रता B, लूप के तल के लम्बवत है। चुम्बकीय क्षेत्र के कारण लूप में लगने वाला बल-आघूर्ण है :
View Solutionत्रिज्या चुम्बकीय क्षेत्र से क्या तात्पर्य है?
View Solutionतार की एक वृत्ताकार कुंडली में 100 फेरे है, प्रत्येक की त्रिज्या 8.0 सेमी है और इनमे 0.40 ऐम्पियर विघुत धारा प्रवाहित हो रही है। कुंडली के केंद्र पर चुम्बकीय क्षेत्र का परिमाण क्या है?
View Solutionजैसे की चित्रित किया गया है। एक सम्मित तारे (symmetric star)के आकार के चालक में अपरिवर्तित धरा ी बह रही है। यहाँ विपरीत शीर्षों (diametrically opposoite vertices) के बीच की दुरी 4a है। चालक के केंद्र पर चुंबकीय क्षेत्र का मान होगा :
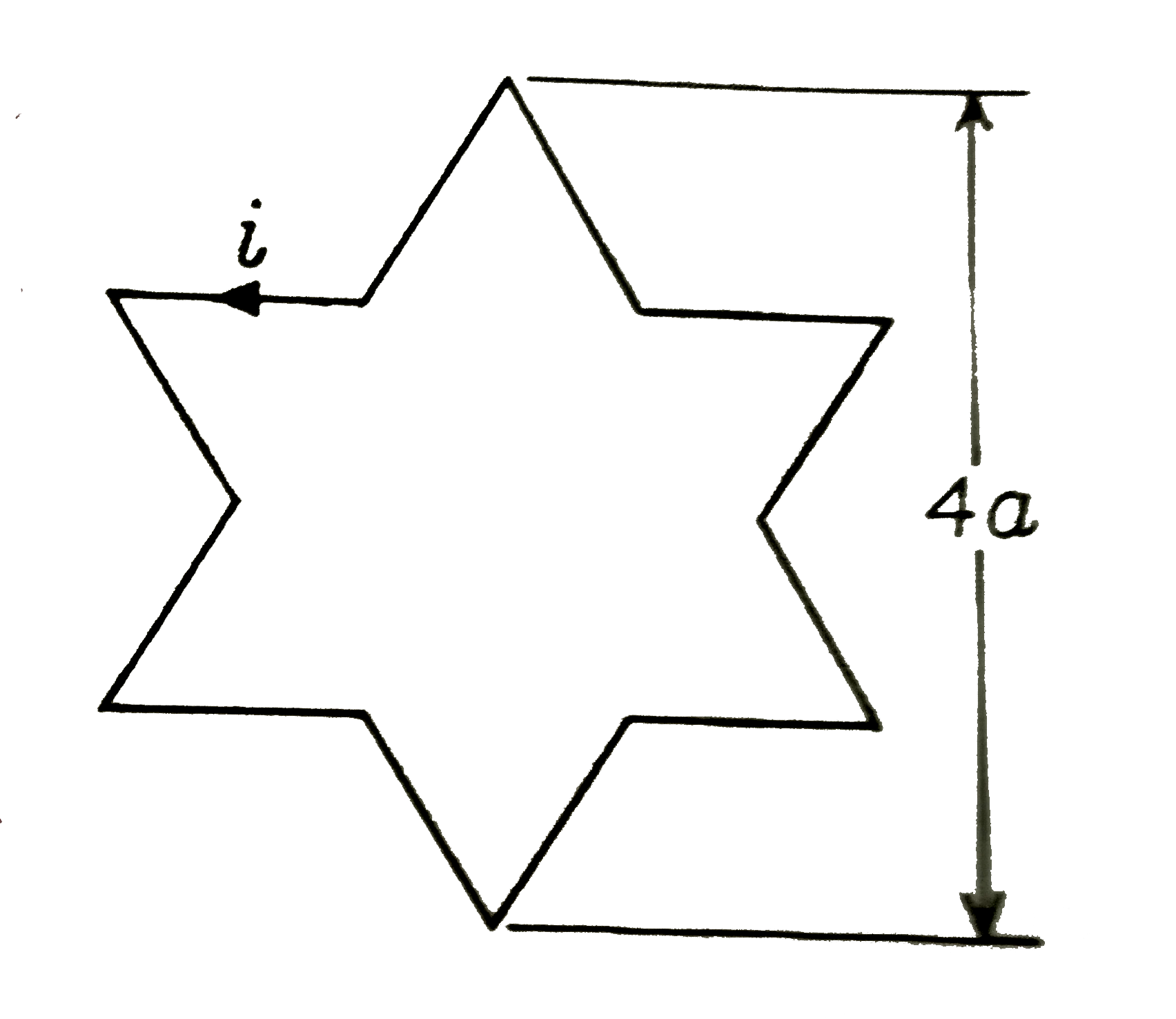
View Solutionग्रीष्म ऋतु की गर्म रात्रि में , भू-तल के निकट , वायु का अपवर्तनांक न्यूनतम होता है । और भू-तल से ऊंचाई के साथ बढ़ता जाता है । यदि , कोई प्रकाश - किरणपुँज क्षैतिज दिशा में जा रहा हो तो हाइगेन्स के सिद्धान्त से यह परिणाम प्राप्त होता है कि, चलते हुए प्रकाश किरणपुँज :
View Solutionवृत्ताकार धारावाही कुंडली के कारण चुम्बकीय क्षेत्र
View Solutionविद्युत धारावाही वृत्ताकार पाश के अक्ष पर चुंबकीय क्षेत्र
View Solutionविद्युत धारावाही वृत्ताकार पाश के अक्ष तथा केन्द्र पर चुंबकीय क्षेत्र | ऐम्पियर का परिपथीय नियम
View Solutionधारावाही वृत्ताकार लूप और कुंडली के केंद्र पर चुंबकीय क्षेत्र
View Solutionधारावाहिक चाप के कारण चुंबकीय क्षेत्र|वृत्ताकार पथ पर आवेश की गति के कारण केंद्र पर चुंबकीय क्षेत्र
View Solutionवृत्ताकार पथ पर आवेश की गति के कारण केंद्र पर चुंबकीय क्षेत्र|धारावाहि चाप के कारण केंद्र पर चुंबकीय क्षेत्र
View Solutionधरावाही वलय के अक्ष पर चुंबकीय क्षेत्र
View Solutionधारावाही वलय के अक्ष पर चुंबकीय क्षेत्र
View Solutionविद्युत धारावाही वृत्ताकार पाश के केन्द्र पर चुंबकीय क्षेत्र
View Solutionविद्युत धारावाही वृत्ताकार पाश के केन्द्र पर चुंबकीय क्षेत्र|आंकीक प्रश्न
View Solutionविद्युत धारावाही वृत्ताकार पाश के अक्ष पर चुंबकीय क्षेत्र
View Solution
