एक समतल विधुतचुम्बकीय तरंग में दोलित चुम्बकीय क्षेत्र द्वारा दिया जाता है । (i) विधुतचुम्बकीय तरंग की तरंगदैघर्य ज्ञात कीजिए । (ii) दोलित वैधुत क्षेत्र का व्यंजक लिकीय ।
(i) चुम्बकिय क्षेत्र की दी गई समीकरण की से तुलना करने पर, जहाँ तथा
अथवा 0.0067 मीटर |
(ii) तथा टेस्ला ।
वोल्ट/मीटर |
दोलित वैधुत क्षेत्र का व्यंजक
वोल्ट/ मीटर ।
Topper's Solved these Questions
- विधुतचुम्बकीय तरंगे BOOK - NOOTAN HINDICHAPTER - विधुतचुम्बकीय तरंगे EXERCISE - एन.सी.ई.आर.टी.प्रश्न
10 Videos
- विधुतचुम्बकीय तरंगे BOOK - NOOTAN HINDICHAPTER - विधुतचुम्बकीय तरंगे EXERCISE - अतिरिक्त प्रश्न
5 Videos
- विद्युतचुम्बकीय प्रेरण BOOK - NOOTAN HINDICHAPTER - विद्युतचुम्बकीय प्रेरण EXERCISE - विविध प्रतियोगी परीक्षाओं के लिए (वस्तुनिष्ठ प्रकार प्रश्न)
23 Videos
- विवर्तनBOOK - NOOTAN HINDICHAPTER - विवर्तनEXERCISE - वस्तुनिष्ट प्रकार प्रश्न
12 Videos
Similar Questions
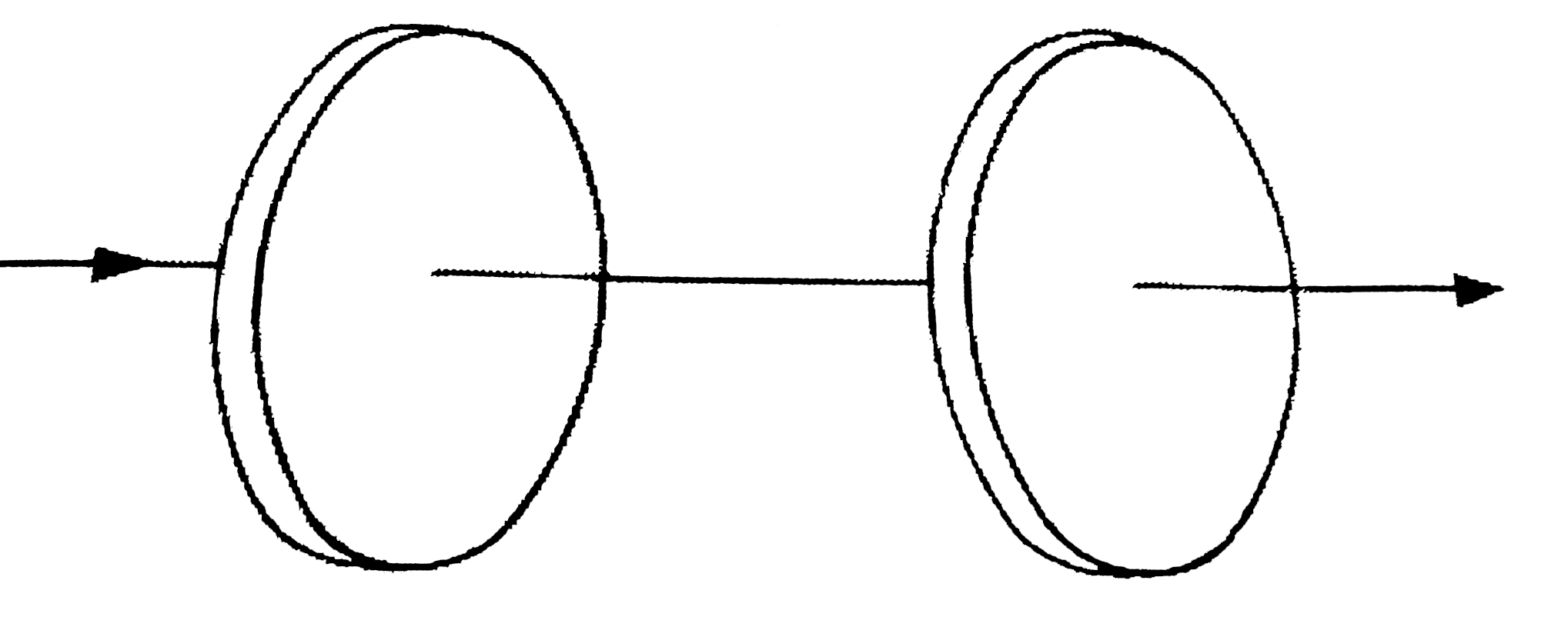
चित्र में एक संधारित दर्शाया गया है, जो 12 सेमी त्रिज्या की दो वृताकार प्लेटो को 5.0 सेमी की दूरी पर रखकर बनाया गया है । संधरित्र को एक बाह्य स्रोत (जो चित्र में नहीं दर्शाया गया है) द्वारा आवेशित किया जा रहा है । आवेशकारी धरा नियत है और इसका मान 0.15 एम्पियर है ।
(a) धारिता एवं प्लेटो के बीच विभवांतर परिवर्तन की दर का परिकलन कीजिए ।
(b) प्लेटो के बीच विस्थापन धारा ज्ञात कीजिए ।
(c) क्या किरचॉफ का प्रथम नियम संधारित्र की प्रत्येक प्लेट पर लागू होता है ? स्पष्ट कीजिए ।
View Solutionकल्पना कीजिए कि निर्वात में एक वैधुतचुम्बकिय तरंग का विधुत क्षेत्र →E={(3.1N/C)cos[1.8rad/m)y+(5.4×106rad/s)t]}ˆi है |
(a) तरंग संचरण कि दिशा क्या है ?
(b) तरंगदैघर्य λ कितनी है ?
(c) आवृति v कितनी है ?
(d) तरंग के चुम्बकिय क्षेत्र सदिश का आयाम कितना है?
(e) तरंग के चुम्बकिय क्षेत्र के लिए व्यंजक लिखिए ।
View Solutionकोई एकसमान चुम्बकीय क्षेत्र r त्रिज्या के किसी क्षेत्र में सीमित है । यह चुम्बकीय क्षेत्र समय के साथ d→B/dt की दर से परिवर्तित होता है । संलग्न आरेख के अनुसार, त्रिज्या R>r का लूप-1, r क्षेत्र को परिबद्ध करता है, तथा R त्रिज्या का लूप - 2, चुम्बकीय क्षेत्र की सीमा के बाहर है । उत्पन्न विo वाo बल का मान होगा :
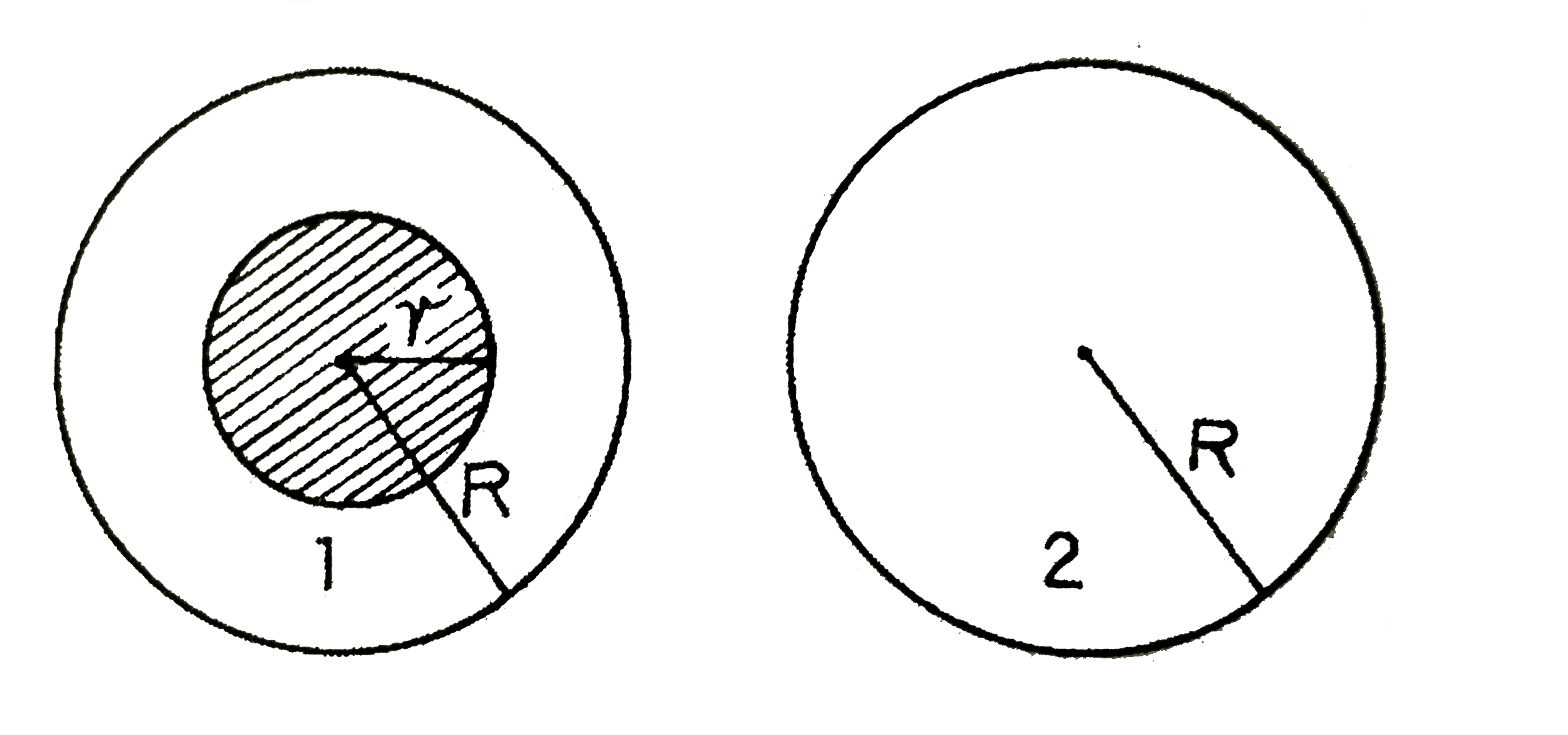
View Solutionएक समान्तर एकवर्गी - पुँज एक पतली स्लिट पर अभिलंबवत गिरता है । पुँज की दिशा के लंबवत रखे एक पर्दे पर विवर्तन - प्रतिरूप बनता है । विवर्तन - प्रतिरूप के प्रथम निमनष्ट पर विवर्तन - प्रतिरूप बनता है विवर्तन प्रतिरूप के प्रथम निम्निष्ट पर स्लिट के दोनों किनारो से आने वाली किरणों के बीच कलान्तर :
View SolutionThe oscillating magnetic field in a plane electromagnetic wave is given by
By=(8×10−6)sin(2×1011t+300πx) T
Calculate the λ of Electromagnetic wave.
View SolutionThe oscillating magnetic field in a plane electromagnetic wave is given by B_(y) = (8 xx 10^(-6)) sin (2 xx 10^(11) t + 300 pi x ) T find the amplitude of electric field.
View Solutionएक समतल विद्युत - चुम्बकीय तरंग में दोलिनी चुम्बकीय क्षेत्र है - By=8×10−6sin(2×1011t+300πx)T तो
विद्युत - चुम्बकीय तरंगदैर्ध्य के गणना कीजिए।
View Solutionएक समतल विद्युत - चुम्बकीय तरंग में दोलिनी चुम्बकीय क्षेत्र है - By=8×10−6sin(2×1011t+300πx)T तो
दोलिनी विद्युत क्षेत्र का समीकरण बताइए।
View Solutionचुम्बकीय क्षेत्र में आवेश की गति
View Solutionचुम्बकीय क्षेत्र तथा चुम्बकीय क्षेत्र की तीव्रता | एक अकेले चुम्बकीय ध्रुव के कारण चुम्बकीय क्षेत्र की तीव्रता
View Solutionएक समान चुम्बकीय क्षेत्र में गतिमान आवेश पर बल | संयुक्त विद्युत चुम्बकीय क्षेत्र में आवेशित कण की गति
View Solutionएक अकेले चुम्बकीय ध्रुव के कारण चुम्बकीय क्षेत्र की तीव्रता | चुम्बकीय द्विध्रुव के कारण अक्षीय स्थिति में चुम्बकीय क्षेत्र की तीव्रता | चुम्बकीय द्विध्रुव के कारण निरक्षीय स्थिति में चुम्बकीय क्षेत्र की तीव्रता
View Solutionचुम्बकीय क्षेत्र में आवेशित कण की गति
View Solutionएकसमान चुम्बकीय क्षेत्र में आवेश की गति
View Solutionचुम्बकीय क्षेत्र में आवेशित कण की गति
View Solution
