एक छोटी वस्तु को 30 सेमी फोकस दुरी वाले एक पतले उत्तल लेन्स की बायीं ओर 50 सेमी की दूरी पर रखा गया है | 100 सेमी की वक्रता त्रिज्या वाले एक उत्तल गोलाकार दर्पण को लेन्स के दायीं ओर 50 सेमी की दूरी पर रखा गया है | दर्पण को इस प्रकार से झुकाया गया है कि दर्पण की अक्ष लेन्स की अक्ष से θ=30∘ का कोण बनती है, जैसा चित्र में दर्शाया गया है
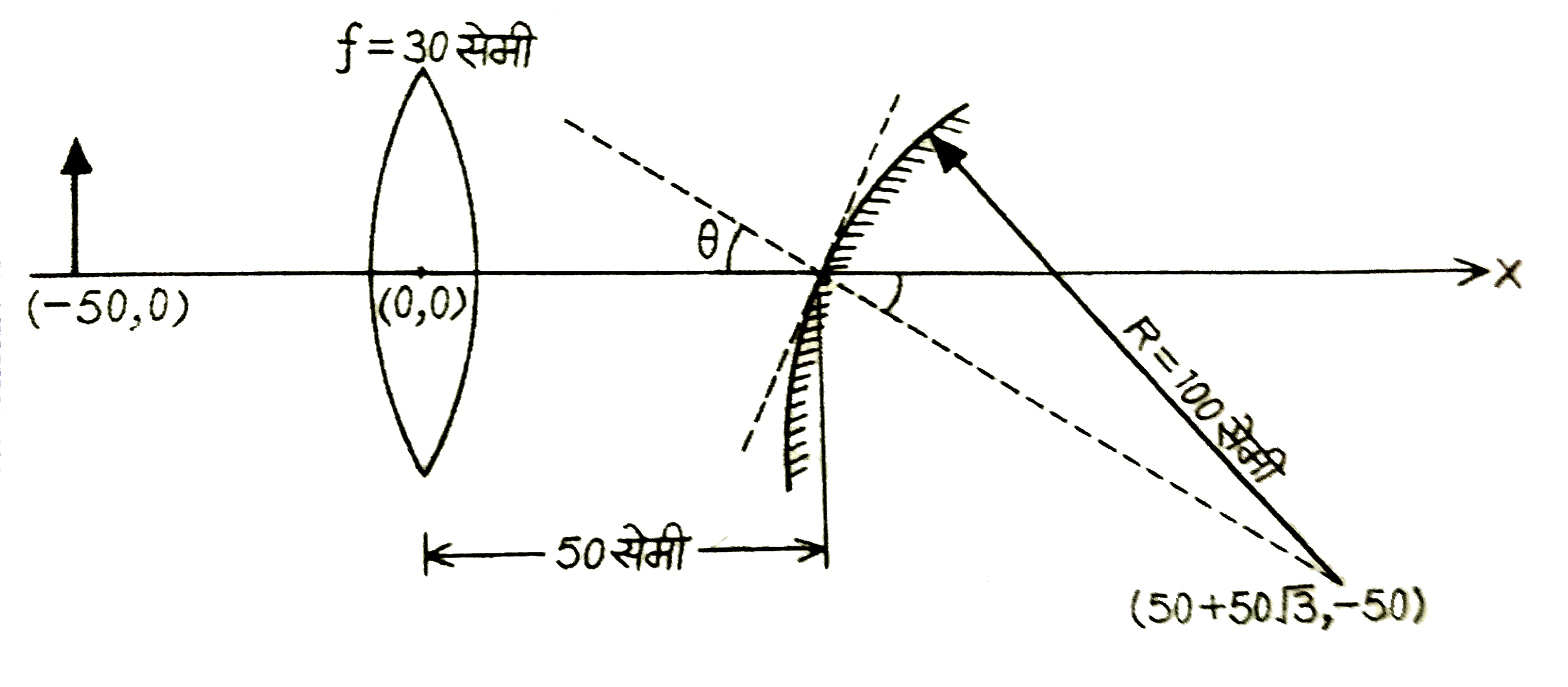
यदि निर्देशांक पद्धति का मूल बिंदु लेन्स के मध्य में हो, तो जहाँ प्रतिबिम्ब बना है उस बिंदु का निर्देशांक (x,y) सेमी में है :
(50−25√25)
(0, 0)
(1253,25√3)
(25,25√3)
The correct Answer is:D
प्रारम्भ करने के लिये माना दर्पण की अक्ष, लेन्स की अक्ष सम्पाती है (अर्थात θ=0 ) लेन्स द्वारा बना प्रतिबिम्ब I1 है
1v1−1(−50)=130 अथवा v1=75 सेमी |
I1 दर्पण के लिये आभासी वस्तु का कार्य करता है |
PI1=−25 सेमी, दर्पण की फोकस दूरी = 50 सेमी
∴1v2+125=150, v2=−50 सेमी |
इस प्रकार , I1 का प्रतिबिम्ब I2 मूल बिंदु (0, 0) पर बनता है |
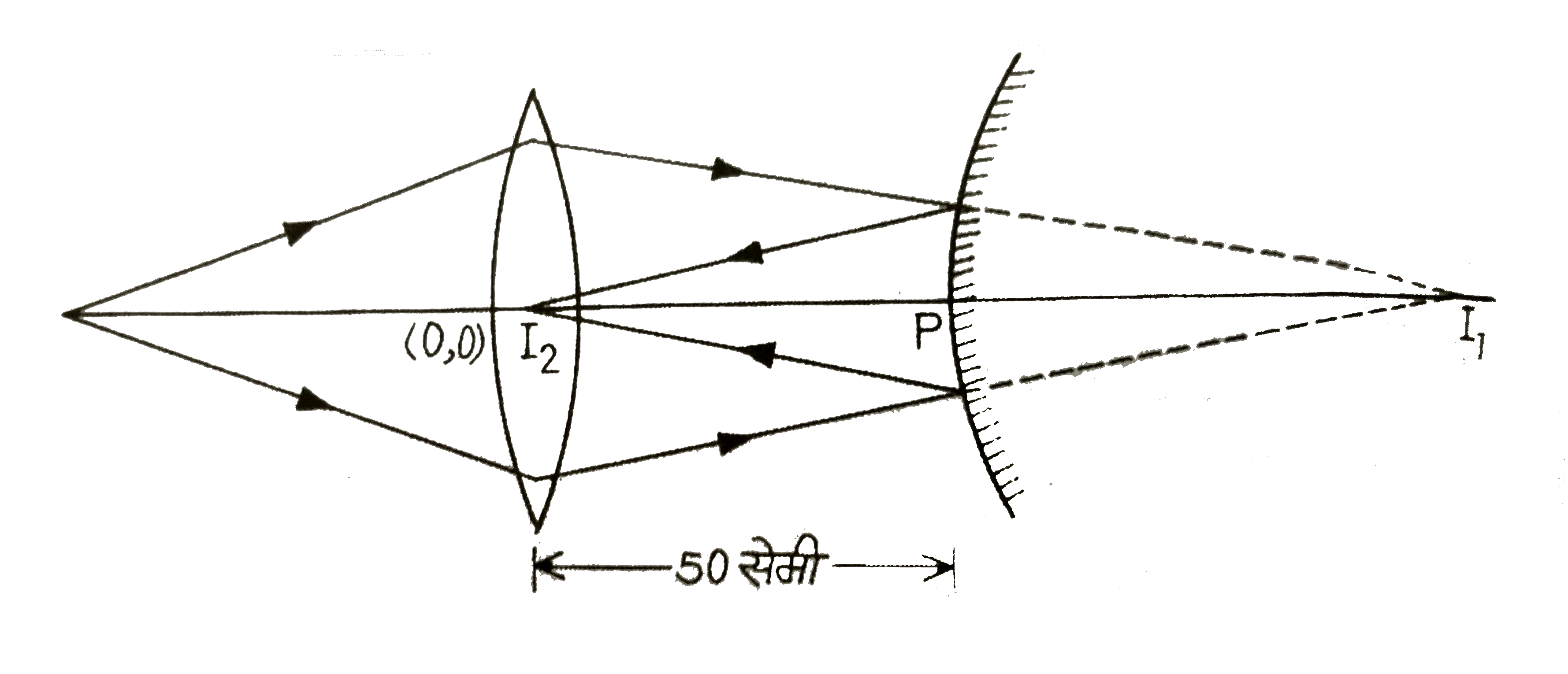
उत्तल दर्पण को घुमाने के लिहाज से समतल दर्पण मानने पर, दर्पण के घुमाव कोण (θ=30∘) के लिये, प्रतिबिम्ब 2thete=60∘ कोण से विक्षेपित होता है , जबकि दर्पण के ध्रुव से प्रतिबिम्ब की दूरी (50 सेमी ) नियत रहती है |
अतः अंतिम प्रतिबिम्ब के x- निर्देशांक =50 सेमी −50cos60∘
= 25 सेमी
अन्तिम प्रतिबिम्ब के y- निर्देशांक =50sin60∘=25√3 सेमी |
Topper's Solved these Questions
- प्रकाश का गोलीय पृष्ठों पर अपवर्तन : लेन्सBOOK - NOOTAN HINDICHAPTER - प्रकाश का गोलीय पृष्ठों पर अपवर्तन : लेन्सEXERCISE - आंकिक
40 Videos
- पृथ्वी का चुम्बकत्व तथा चुम्बकीय पदार्थ BOOK - NOOTAN HINDICHAPTER - पृथ्वी का चुम्बकत्व तथा चुम्बकीय पदार्थ EXERCISE - विविध प्रतियोगी परीक्षाओं के लिए (वस्तुनिष्ठ प्रकार प्रश्न) (एकल उत्तर प्रकार)
6 Videos
- प्रकाश का ध्रुवणBOOK - NOOTAN HINDICHAPTER - प्रकाश का ध्रुवणEXERCISE - विविध प्रतियोगिता परीक्षाओं के लिए (वस्तुनिष्ठ प्रकार प्रश्न )
6 Videos
Similar Questions
काँच के 4.0 सेमी व्यास के एक ठोस के गोले के भीतर वायु का बुलबुला गोले के पृष्ट से 1.2 सेमी की दूरी पर स्थित हैं | गोले के व्यास के अनुदिश बुलबुले के प्रतिबिम्ब की स्थिति ज्ञात कीजिए , जब उसे निकट वाले पृष्ठ से देखा जाता है,| (काँच का अपवर्तनांक n = 1.5)
View Solutionकिसी विद्युत-चुम्बक के ध्रुवों के बीच प्रतिचुम्बकीय पदार्थ की एक पतली छड़ ऊर्ध्वाधर स्थित है। जब विद्युत-चुम्बक में धारा प्रवाहित की जाती है, तो वह छड़ क्षैतिज चुम्बकीय क्षेत्र से बाहर ऊपर की और धकेल दी जाती है। इस प्रकार यह छड़ गुरुत्वीय स्थितिज ऊर्जा प्राप्त करती है। ऐसा करने के लिए आवश्यक कार्य करता है:
View Solutionअपवर्तनांक 'n' वाले पदार्थ के किसी समतल पृष्ठ पर कोई अध्रुवित प्रकाश वायु से आपतन कोण (i) पर यह पाया गया कि परावर्तित किरणे और अपवर्तित किरणे एक-दूसरे के लंबवत हैं। निम्नलिखित में से कौन-सा विकल्प इस स्थिति में सही है ?
View Solutionएक बिंदु वस्तु एक काँच जिसका अपवर्तनांक (μs=32) है, से बने 20 सेमी फोकस दूरी वाले उत्तल लेन्स से 30 सेमी की दूरी पर रखी है। वस्तु का अन्तिम प्रतिबिमब अनन्त पर बनेगा यदि
View Solutionएक दीर्घवृत्त एक धागे से निर्मित किया जाता है, जिसके सिरों को दो पिनों द्वारा स्थिर बिंदुओं S और S' से बाँध दिया है। अब एक पेन्सिल की नोंक से धागे को तानकर उसे कागज पर इस प्रकार चलाया की धागा तना रहे। यदि इस प्रकार बने दीर्घवृत्त के अक्ष क्रमशः 6 सेमी तथा 4 सेमी हों, तो धागे की लम्बाई और पिनों के बीच की दूरी ज्ञात कीजिए।
View Solutionदो वृत्तों, जिनकी त्रिज्याएँ क्रमशः सेमी 1.7 और 2.8 सेमी की है, की एक उभयनिष्ठ तिर्यक स्पर्श रेखा की रचना कीजिए जबकि दोनों के केंद्र एक दूसरे से 6 सेमी दूरी पर है।
View Solutionएक वृत्त 3 सेमी त्रिज्या को खींचिए। जिसके केंद्र O से 5 सेमी दूरी स्थित P से दो स्पर्श रेखाओ की रचना कीजिए।
View Solutionदो वृत्तों, जिनकी त्रिज्याएँ क्रमशः सेमी 1.7 और 2.8 सेमी की है ,की एक उभयनिष्ठ तिर्यक स्पर्श रेखा की रचना कीजिए जबकि दोनों के केंद्र एक दूसरे से 6 सेमी दूरी पर है।
View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
View Solutionएक समबाहु त्रिभुज की भुजाएँ 2 सेमी/से की दर से बढ़ रही है। क्षेत्रफल के बढ़ने की दर, जबकि भुजा 10 सेमी हो, है
View Solutionएक द्विध्रुव 10 सेमी लम्बा तथा आवेश 500μC से बना है। इसके अक्ष से 25 सेमी दूरी पर विद्युत क्षेत्र की तीव्रता होगी
View Solutionएक घन के विकर्ण की लम्बाई 12√3 सेमी है। घन के कोर की लम्बाई .............होगी।
View Solutionएक शंकु की त्रिज्या 7 सेमी और ऊँचाई 9 सेमी है। इसका आयतन समान त्रिज्या वाले एक दूसरे शंकु के वक्र पृष्ठ के बराबर होता है। इस शंकु को तिर्यक ऊँचाई ज्ञात कीजिए।
View Solutionयदि वृत्त के केंद्र से 3 सेमी. की दूरी पर स्थित जीवा की लम्बाई 8 सेमी. है, तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionसंपर्क में रखे दो पतले लेंसों की संयुक्त फोकस दूरी|उत्तल लेंस तथा समतल दर्पण का संयोजन#!#लेंसों के उपयोग
View Solutionएक लेंस 10 सेमी दूरी पर रखी वस्तु का तीन गुना बड़ा आभासी प्रतिबिम्ब बनाता है। लेंस की प्रकृति, फोकस दूरी तथा प्रतिबिम्ब की स्थिति ज्ञात कीजिए।
View Solution
