चित्र में कोई समोत्तल लेंस (अपवर्तनांक 1.50) किसी समतल दर्पण के फलक पर द्रव की परत के संपर्क में दर्शाया गया है कोई छोटी सुई जिसकी नोक अक्ष पर है अक्ष के अनुदिश ऊपर - नीचे गति कराकर इस प्रकार समायोजित की जाती है की सुई की नोंक का उल्टा प्रतिबिम्ब सुई की स्थिति पर ही बने । इस स्थिति में सुई की लेंस से दूरी 45.0 सेमी है । द्रव को हटाकर प्रयोग को दोहराया जाता है दूरी 30.0 सेमी मापी जाती है । द्रव का अपवर्तनांक क्या है ?

निकाय की तुल्य फोकस - दूरी
1f=2(1fg+1fl) . . . (i)
सूत्र में 2 इस कारण लिया गया है, क्योकि प्रकाश की किरण प्रत्येक लेंस में से दो बार गुजरती है
P से चलने वाली प्रकाश की किरणे समतल दर्पण पर अभिलंबवत पड़ती है तथा दर्पण से परावर्तन के पश्चात उसी मार्ग से वापस लौट जाती उसी स्थान पर प्रतिबिम्ब बनाती है कांच व द्रव लेंसों से गुजरने के पश्चात् वे समांतर हो जाएगी। यह तब ही संभव है जबकि पिन लेंस निकाय के प्रथम फोकस पर स्थित है ।
काँच के लेंस के लिये, यदि प्रत्येक पृष्ठ की त्रिज्या R हो तथा लेंस की फोकस - दूरी fg हो तो
1fg=(ng−1)(1R1−1R2)
=(1.5−1)(2R)=1R
∴fg=R . . . (ii)
द्रव लेंस के लिये 1fl=(nl−1)(1R1−1R2)
यहाँ R1=−R तथा R2=∞
∴1fl=(nl−1)(1−R)=−nl−1R . . . (iii)
स्पष्ट है द्रव लेंस अवतल है, f=45.0 सेमी
1f=2(1fg+1fl)
145.0=2[1R−(nl−1)R]=2R[2−nl] . . . (iv)
जब द्रव को हटा दिया जाता है f′=30.0 सेमी
∴1f′=2(1fg)=2R
∴R=2×f′=2×30.0=60.0 सेमी
यह मान समीकरण (iv) में रखने पर
145.0=260.0(2−nl)
nl=43=1.33.
Topper's Solved these Questions
- प्रकाशित यंत्र BOOK - NOOTAN HINDICHAPTER - प्रकाशित यंत्र EXERCISE - प्रश्नावली
8 Videos
- प्रकाशित यंत्र BOOK - NOOTAN HINDICHAPTER - प्रकाशित यंत्र EXERCISE - अतिलघु उत्तरीय
12 Videos
- प्रकाशित यंत्र BOOK - NOOTAN HINDICHAPTER - प्रकाशित यंत्र EXERCISE - वस्तुनिष्ठ प्रकार प्रश्न ( एकल उत्तर प्रकार )
5 Videos
- प्रकाशवैधुत प्रभाव : द्रव्य तरंगें BOOK - NOOTAN HINDICHAPTER - प्रकाशवैधुत प्रभाव : द्रव्य तरंगें EXERCISE - विविध प्रतियोगी परीक्षाओं के लिए (वस्तुनिष्ठ प्रकार प्रश्न ) (एकल उत्तर प्रकार )
28 Videos
- प्रत्यावर्ती धाराBOOK - NOOTAN HINDICHAPTER - प्रत्यावर्ती धाराEXERCISE - वस्तुनिष्ठ प्रकार प्रश्न
16 Videos
Similar Questions
सामान्य नेत्र के लिए स्पष्ट दृष्टि की न्यूनतम दूरी है :
View Solutionचन्द्रमा का आकर तारो से बहुत छोटा है परन्तु फिर भी यह बड़ा दिखाई पड़ता है , क्यों ?
View Solutionयदि अभिदृश्यक लेंस की फोकस दूरी बढ़ा दिया जाये, तो :
View Solutionचित्र में तीन विभिन्न आपतित विकिरणों के लिए, एक फोटो-सुग्राही पृष्ठ से प्राप्त प्रकाशवैधुत धारा तथा एनोड विभव के बीच ग्राफ दर्शाये गये हैं । माना कि वक्रों a, b, c के संगत , आपतित विकिरणों कि तीव्रताएँ क्रमशः Ia,Ib,Ic हैं तथा आवृत्तियाँ क्रमशःfa,fb,fc हैं । निम्नलिखित में कौन-सा कथन सत्य है ?
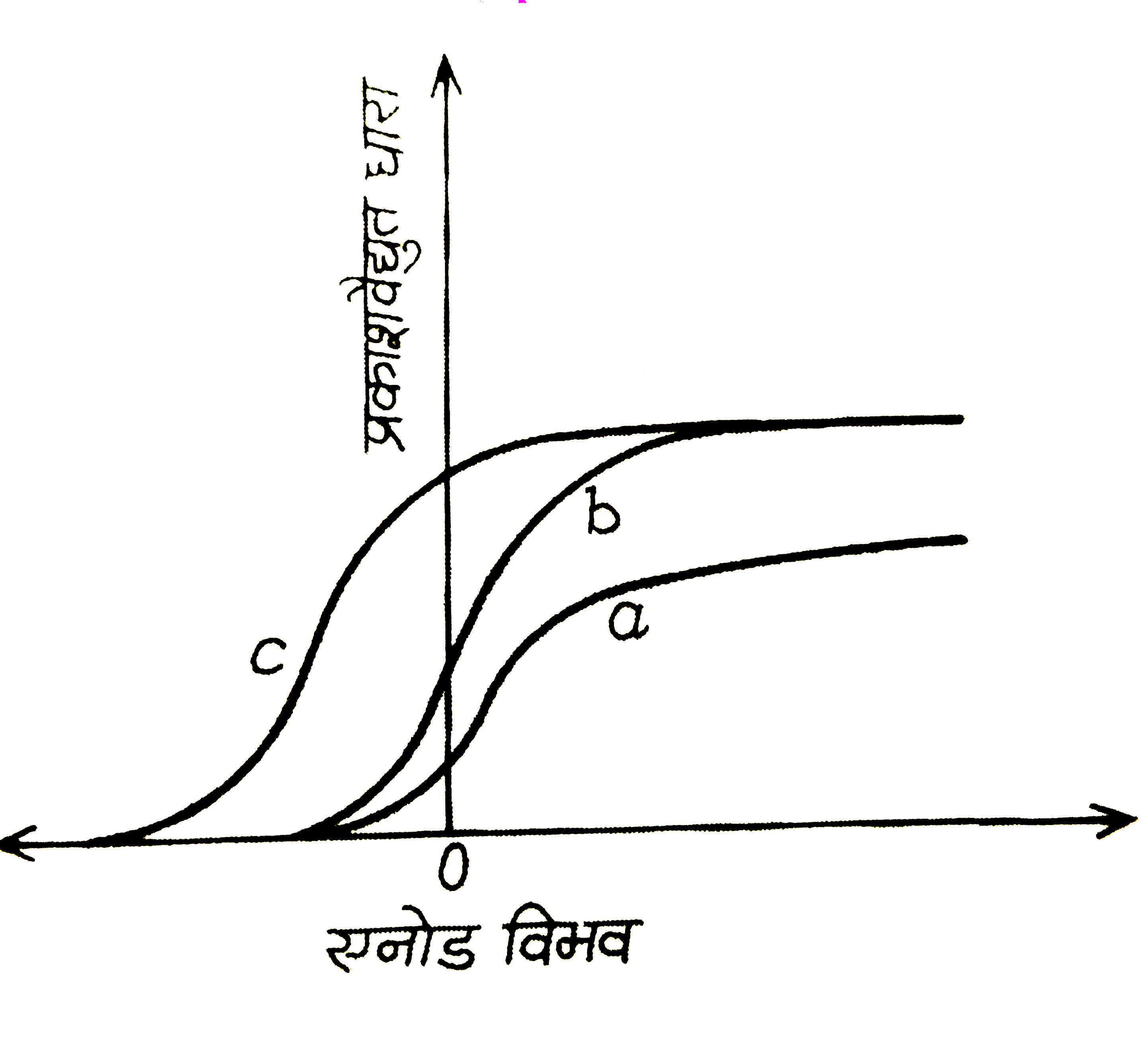
View Solutionएक लधु सिग्नल वोल्टता किसी आदर्श सधारित्र C के सिरों पर लगाया गया है
View Solutionयह ज्ञात है की महाविद्यालय के छात्रों में से 60 % छात्रावास में रहते है और 40 % छात्रावास में नहीं रहते है । पूर्ववर्ती वर्ष से परिणाम सूचित करते है की छात्रावास में रहने वाले छात्रों में से30 % छात्रों में से 20 % छात्रों ने A ग्रेड लिए। वर्ष के अंत में महाविद्यालय के एक छात्र को यादृच्छया चुना गया और पाया गया की उसे A ग्रेड मिला है । इस बात की क्या प्रायिकता है की वह छात्रावास में रहने वाला है ?
View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
View Solutionयदि एक अतिपरवलय के संयुग्मी अक्ष की लम्बाई 5 है तथा इसकी नाभिको के बीच की दुरी 13 है, तो इस अतिपरवलय की उत्केंद्रता है
View Solutionमाना एक दीर्घवृत्त जिसका दीर्घ -अक्ष, X-अक्ष के अनुदिश है तथा केन्द्र मूलबिंदु पर है, के नाभिलम्ब की लम्बाई 8 है । यदि दीर्घवृत्त की नाभियो के बीच की दुरी, इसके लघु-अक्ष की लम्बाई के समान हो, तो निम्न में से कौन-सा बिन्दु इस पर स्थित है?
View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
View Solutionउत्तल लेंस द्वारा वस्तु के विभिन्न स्थितियों में प्रतिबिम्ब की प्रकृति, स्थिति तथा आकार
View Solutionसंपर्क में रखे दो पतले लेंसों की संयुक्त फोकस दूरी|उत्तल लेंस तथा समतल दर्पण का संयोजन#!#लेंसों के उपयोग
View Solutionएक लेंस 10 सेमी दूरी पर रखी वस्तु का तीन गुना बड़ा आभासी प्रतिबिम्ब बनाता है। लेंस की प्रकृति, फोकस दूरी तथा प्रतिबिम्ब की स्थिति ज्ञात कीजिए।
View Solutionसमतल दर्पण से प्रतिबिंब का बनना#!#प्रतिबिंबो की संख्या#!#वस्तु या दर्पण की स्थिति में परिवर्तन के कारण प्रतिबिंब की स्थिति पर प्रभाव
View Solutionनाभिक से दूरी पर, अनंतसूक्ष्म मोटाई dr के गोलीय कोश में हाइड्रोजन परमाणु के 1s इलेक्ट्रॉन के पाए जाने की प्रायिकता P है। इस कोश का आयतन 4rr2 dr है। r पर P की निर्भरता का गुणात्मक रेखाचित्र है-
View Solutionएक स्थिर आयतन ऊष्मातापी में अणुभार 28 की एक गैस के 3.5 gको 298.0K पर ऑक्सीजन के अधिवाकय में जलाया गया था दहन प्रक्रम के कारण उष्मामापी के टप्प 298.0K से 298.45 K तक की वृद्धि पायी गयी दिया हुआ है की उष्मामापी की उष्मा धारिता 2.5 kg K^-1 है गैस के दहन की अन्थेलपी का संख्यात्मक मान में है
View Solution
