इस शताब्दी के एक महान भौतिकविद (पी.ए.एम. डिरेक) प्रकृति के मूल स्थिरांको (नियतांकों) के आंकिक मानो के साथ क्रीड़ा में आनंद लेते थे । इससे उन्होने एक बहुत ही रोचक प्रेक्षण किया । परमाण्वीय भौतिकी के मूल नियतांकों (जैसे - इलेक्ट्रॉन का द्रव्यमान, प्रोटॉन का द्रव्यमान तथा गुरुत्वीय नियतांक G) से उन्हें पता लगा की वे एक ऐसी संख्या पर पहुंच गए हैं जिसकी विमा समय की विमा है । साथ ही, यह एक बहुत ही बड़ी संख्या थी और इसका परिमाण विश्व की वर्तमान आकलित आयु (~ 1500 करोड़ वर्ष) के करीब है । इस पुस्तक में दी गई मूल नियतांकों की सारणी के आधार पर यह देखने का प्रयास कीजिए की क्या आप भी यह संख्या (या और कोई अन्य रोचक संख्या जिसे आप सोच सकते हैं) बना सकते हैं ? यदि विश्व की आयु तथा इस संख्या में समानता महत्वपरून है, तो मूल नियतांकों की स्थिरता किस प्रकार प्रभावित होगी ?
इलेक्ट्रॉन व प्रोटॉन के बीच गुरुत्वीय बल,
Fg=Gmempr2 ...(i)
इलेक्ट्रॉन व प्रोटॉन के बीच वैधुत बल,
Fe=14πε0(e)(e)r2=14πε0e2r2 ...(ii)
बल, F=F2eFG=(14πε0e2r2)2Gmempr2
=e4(16π2ε20)×(Gmemp)r2 ...(iii)
परन्तु बल (F) की विमा F=[MLT−2] ...(iv)
समीकरण (iv) में M के स्थान पर me तथा L के स्थान पर r रखने पर,
F=[merT−2]
यह मान () में रखने पर, merT−2=e4(16π2ε20)×(Gmemp)r2
अथवा T−2=e4(16π2ε20)Gm2empr3 ...(iv)
अब प्रकाश की चाल (c) की विमा c=[LT−1]
L के स्थान पर r रखने पर, r=[cT]
यह मान समीकरण (v) में रखने पर,
T−2=e4(16π2ε20)×(Gm2emp)×(cT)3
अथवा T=e4(16π2ε20)×(Gm2emp)(c)3
उपरोक्त व्यंजक से प्राप्त समय T लगभग 2.18×1016 सेकंड है जो की पृथ्वी की आयु की कोटि है । अत: मूल स्थिरांको के मान इस प्रकार बदलते हैं की राशि T नियत रहे ।
Topper's Solved these Questions
- विमीय विश्लेषण BOOK - NOOTAN HINDICHAPTER - विमीय विश्लेषण EXERCISE - एन.सी.ई.आर.टी.प्रश्न
24 Videos
- मात्रक, मापन तथा त्रुटि विश्लेषण BOOK - NOOTAN HINDICHAPTER - मात्रक, मापन तथा त्रुटि विश्लेषण EXERCISE - विविध प्रतियोगी परीक्षाओं के लिए (वस्तुनिष्ठ प्रकार प्रश्न)
19 Videos
- वृत्तीय गति BOOK - NOOTAN HINDICHAPTER - वृत्तीय गति EXERCISE - अतिरिक्त प्रशन
17 Videos
Similar Questions
रिक्त स्थान भरिए :
(a) किसी 1 cm भुजा वाले घन का आयतन ...................m3 के बराबर है ।
(b) किसी 2 cm त्रिज्या व 10 cm ऊँचाई वाले सिलिंडर का पृष्ठ क्षेत्रफल...............(mm)2 के बराबर है ।
(c) कोई गाड़ी 18 km/h की चाल से चल रही है तो यह 1 s में ..............m चलती है ।
(d) सीसे का आपेक्षिक घनत्व 11.3 है । इसका घनत्व .......... g cm−3 या ................. kg m−3 है ।
View Solutionदो वर्नियर कैलिपर्स इस तरह से हैं कि उनके मुख्य पैमाने का 1 समी, 10 समभागों में विभाजित है। एक कैलिपर (C1) के वर्नियर पमाने पर 10 बराबर भाग हैं जो कि मुख्य पैमा के 9 भागों के बराबर है। दूसरे कैलिपर (C2) के वर्नियर पैमाने पर भी 10 बराबर भाग हैं जो कि मुख्य पैमाने के 11 भागों के बराबर हैं। दोनों कैलिपर्स के पठनों को चित्र में दर्शाया गया है। C1 तथा C2 द्वारा मापे गए सही मान (सेमी में) क्रमश: हैं :
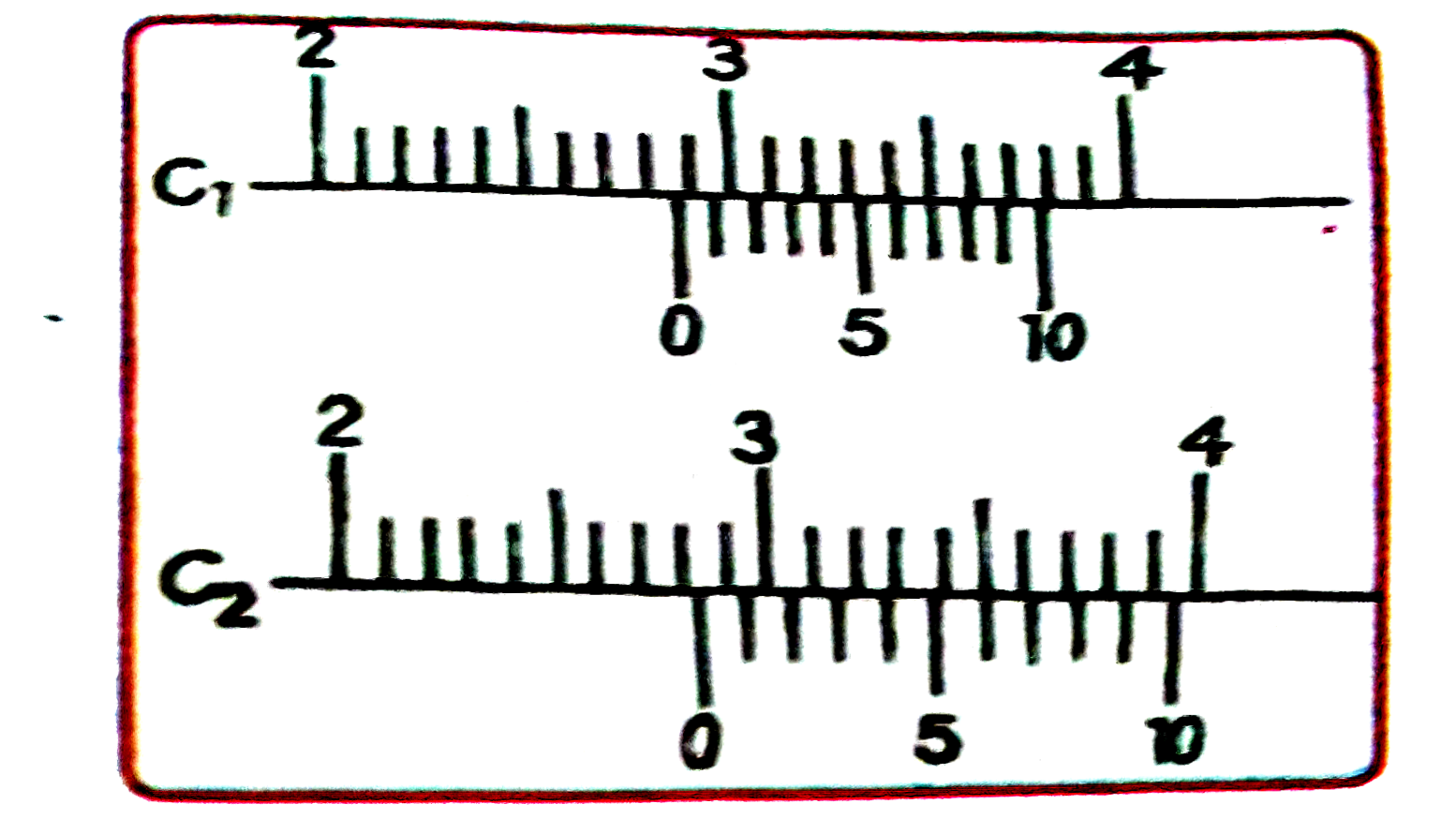
View Solutionचित्र में 0.04 kg सहती के किसी पिंड का स्थिति - समय ग्राफ दर्शाया जय है । इस गति के लिए कोई उचित भौतिक संदर्भ प्रस्तावित कीजिय। पिंड द्वारा प्राप्त दो क्रमिक आवेगों के बिच समय-अंतराल क्या है ? प्रत्येक आवेग का परिमाण क्या है ?

View Solutionएक छोटी फर्म सोने के अंगूठियां और चेनों का निर्माण करती है| प्रतिदिन अंगूठियों और चेनों के निर्माण की कुल संख्या अधिकतम 24 है| एक अंगूठी बनाने में एक घंटा तथा के चेन के बनाने में 30 मिनट लगते है| प्रतिदिन उपलब्ध घंटों की अधिकतम संख्या 16 है|यदि अंगूठी पर लाभ रु 300 तथा एक चेन पर लाभ रु 190 हो, तो ज्ञात कीजिए| की प्रतिदिन कितनी अंगूठियों और चेनों का निर्माण किया जाय ताकि अधिकतम लाभ कमाया जा सकें|
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionद्विघात समीकरण के मूल|द्विघात समीकरण के मूलों की प्रकृति
View Solutionपृथ्वी के गुरुत्वीय बल के प्रभाव में वस्तुओ की गति |प्रश्न |द्रव्यमान |OMR|Summary
View Solution1.0 mg के द्रव्यमान वाले एक कण का वेग 3600 km/h है। कण के तरंग दैर्ध्य की गणना कीजिए।
View Solutionआण्विक द्रव्यमान 390 वाले एक यौगिक को प्राप्त करने के लिए आण्विक द्रव्यमान 180 वाले एक यौगिक को CH_(3)COCl के साथ ऐसिलीकृत किया जाता है। पूर्व यौगिक के प्रति अणु पर उपस्थित ऐमीनो समूहों की संख्या है:
View SolutionAuCl−4 के विलयन से स्वर्ण के 78 g का निक्षेपण करने में, 6.00 A की एक समरूप धारा को कितना समय लगेगा? साथ ही साथ सेल के द्रव्यमान = 197)
View Solutionएक परमाणु में, दो इलेक्ट्रॉन नाभिक के चारों त्रिज्या r और 4r की वृत्ताकार कक्षाओं में परिक्रमण करते हैं। एक परिक्रमण को पूर्ण करने के लिए उनके द्वारा लिए गए समय का अनुपात (T_2 : T_1) है:
View Solutionएक आदर्श गैस के लिए चक्र के सिरों पर दिखाए गए परिवर्तन की एक श्रेणी के माध्यम से किया गया कुल कार्य निम्न के बराबर है:
View Solutionरेडियो नाभिक 90234Th के दो क्रमिक β -क्षय के बाद एक -क्षय के माध्यम से एक नया रेडियो नाभिक प्राप्त किया जाता है। परिणामी रेडियो नाभिक का परमाणु क्रमांक और द्रव्यमान संख्या क्रमश: है:
View Solutionकिसकी उपस्थिति में मूल सिल्वर धातु, NaCN के एक तनु जलीय विलयन के साथ जल में घुलनशील संकुल बनाती है?
View Solutionसल्फर के एक यौगिक में द्रव्यमान द्वारा 8% सल्फर उपस्थित होता है। यौगिक के न्यूनतम आण्विक द्रव्यमान की गणना कीजिए।
View Solution
