In the given figure, ACDB is the diameter of the circle such that AC=CD=DB. Three semicircles are drawn by taking AC,CD,and DB as diameters. What is the ratio of the area of shaded portion to the area of non-shaded portion?
Area of shaded region=π2(AB)24−π2(AB3⋅12)2.
Area of non shaded region=π2(AB2)2+π2(AB3⋅12)2
Ratio=shaded/non shaded.
=π2(AB)24−π2(AB3⋅12)2π2(AB2)2+π2(AB3⋅12)2
=45.
Similar Questions
Knowledge Check
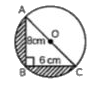
The area of the shaded portion in the figure is
 A7.5π square unitsB6.5π square unitsC5.5π square unitsD4.5π square units
A7.5π square unitsB6.5π square unitsC5.5π square unitsD4.5π square units
In the figure, the area of the shaded portion is :
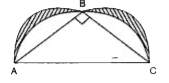
View SolutionIn the given figure, ABC is a right angled triangle with B as right angle. Three semicircles are drawn with AB, BC and AC as diameters. What is the area of the shaded portion, if the area of ΔABC is 12 square units ?
View SolutionIn Fig. 8.8, what is the ratio of the areas of

shaded portions I and II taken together and shaded portion III?
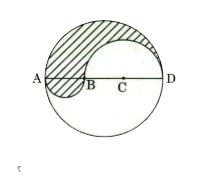
View SolutionABCD is a diameter of a circle of radius 6 cm such that AB = BC = CD. Semicircles are drawn on AB and BD as diameters, as shown in the given figure. Find the area of the shaded region.

View SolutionIn the figure given below, ABCD is the diameter of a circle of radius 9 cm. The lengths AB, BC and CD are equal. Semicircles are drawn on AB and BD as diameters as shown in the figure. What is the area of the shaded region ?
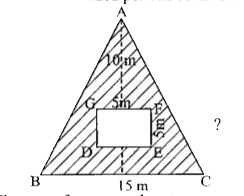
View SolutionQ.49 The area of the shaded portion in the given figure is
View SolutionArea of the shaded portion of the following figure
View Solution


