If S is the sum to infinity of a G.P. whose first term is 'a', then the sum of the first n terms is
(A) S(1−aS)n (B) S[1−(1−aS)n] (C) a[1−(1−aS)n] (D) S[1−(1−Sa)n]
In a GP of the first term a and common ratio r, sum S to the infinity is given by,
S=a1−r⇒1−r=aS⇒r=1−aS.
∴Sum of n terms, Sn=a(1−rn)1−r
Sn=a[1−(1−aS)n]aS=S[1−(1−aS)n]
so, option B is the correct answer.
Similar Questions
If m and x are two real numbers where m∈I, then e2micot−1x(x⋅i+1x⋅i−1)m
(A) cosx+isinx (B) m2 (C) 1 (D) m+12
View SolutionSum of the series 1+2^2x+3^2x^2+4^2x^3+.....to oo , |x| (A) (1+x)/(1-x)^3 (B) (1-x)/(1+x)^3 (C) (2+x)/(1-x)^3 (D) (1-x)/(1+x)^2
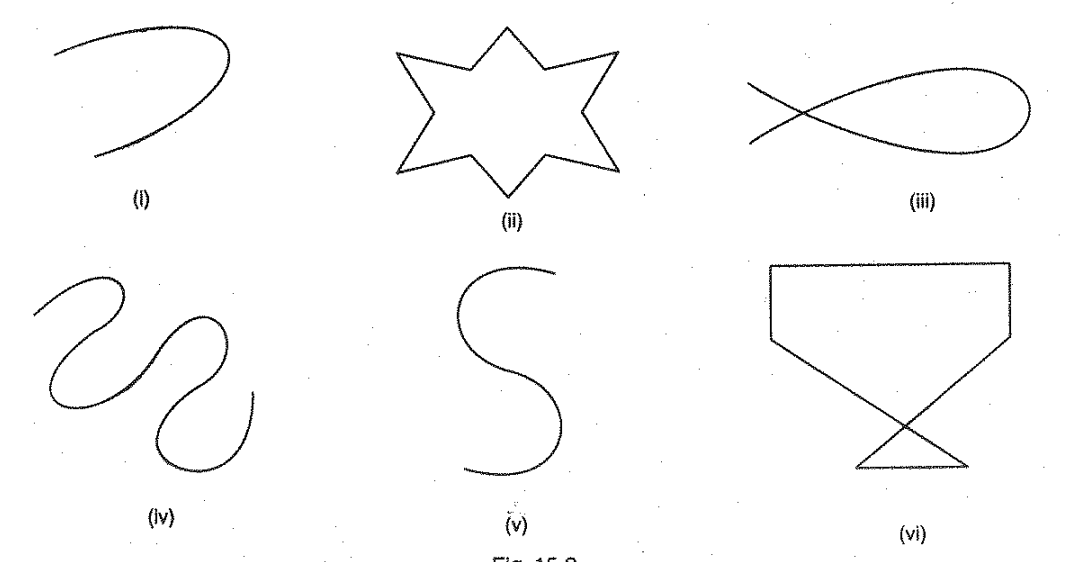
View SolutionClassify they following curves as open or closed:
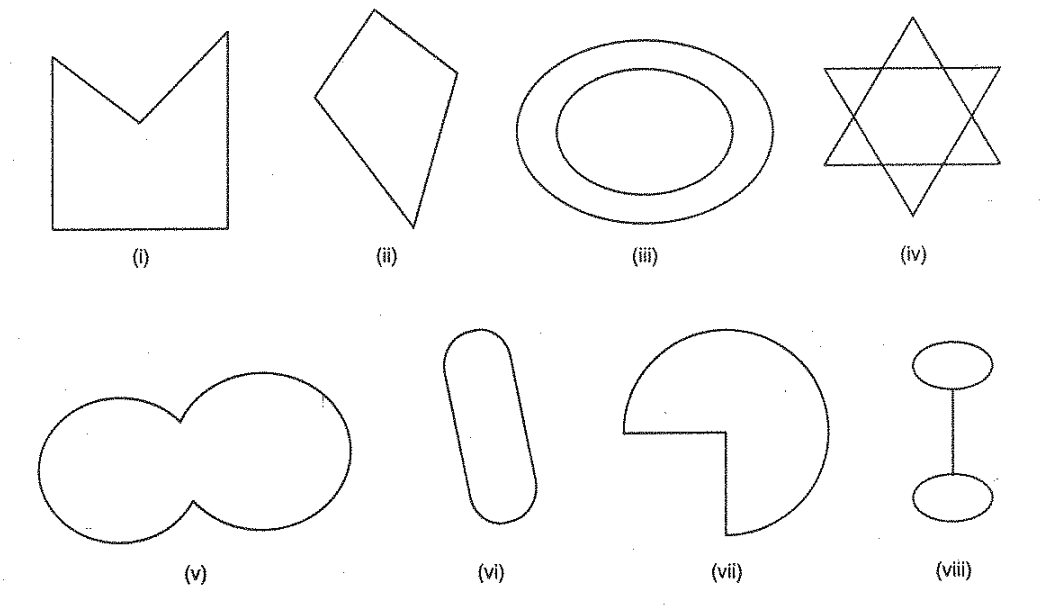
View SolutionFollowing are some figures: Classify each of these figures on the basis of the following:(i) Simple curve (ii) Simple closed curve (iii) Polygon (iv) Convex polygon (v)Concave polygon (vi) Not a curve
View SolutionIf the lines ax+y+1=0, x+by+1=0 and x+y+c=0, (a,b,c being distinct and different from 1) are concurrent, then 11−a+11−b+11−c=
(A) 0 (B) 1 (C) 1a+b+c (D) None of these
View SolutionIf m and x are two real numbers where m∈I, then e2micot−1x(x⋅i+1x⋅i−1)m
(A) cosx+isinx (B) m2 (C) 1 (D) m+12
View SolutionIf m and x are two real numbers where m∈I, then e2micot−1x(x⋅i+1x⋅i−1)m
(A) cosx+isinx (B) m2 (C) 1 (D) m+12
View SolutionIf m and x are two real numbers where m∈I, then e2micot−1x(x⋅i+1x⋅i−1)m
(A) cosx+isinx (B) m2 (C) 1 (D) m+12
View Solution
