Find the maximum value of √3sinx+cosxandx for which a maximum value occurs.
Video Solution
Text Solution
The correct Answer is:Max, value=2 when x=60∘
√3sinx+cosx=2(√32sinx+12sinx)=2sin(x+π6)
Which is maximum when x+π/6=π/2 or x=60∘ and has a maximum value 2.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Exercise 3.27videos
TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULAS
- BOOK - CENGAGECHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Exercise 3.313videos
TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULAS
- BOOK - CENGAGECHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Matrix Match Type1videos
TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULAS
- BOOK - CENGAGECHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - SINGLE CORRECT ANSWER TYPE38videos
TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGECHAPTER - TRIGONOMETRIC RATIOS FOR COMPOUND, MULTIPLE, SUB-MULTIPLE ANGLES, AND TRANSFORMATION FORMULAS EXERCISE - Multiple Correct Answers Type6videos
TRIGONOMETRIC RATIOS FOR COMPOUND, MULTIPLE, SUB-MULTIPLE ANGLES, AND TRANSFORMATION FORMULAS
Similar Questions
Knowledge Check
- Question 1 - Select One
The maximum value of f(x)=sinx(1+cosx) is
A3√34B3√32C3√3D√3 - Question 2 - Select One
Maximum value of f(x)=sinx+cosx is :
A1B2C1√2D√2 - Question 3 - Select One
Which has maximum pKa value ?
A B
B C
C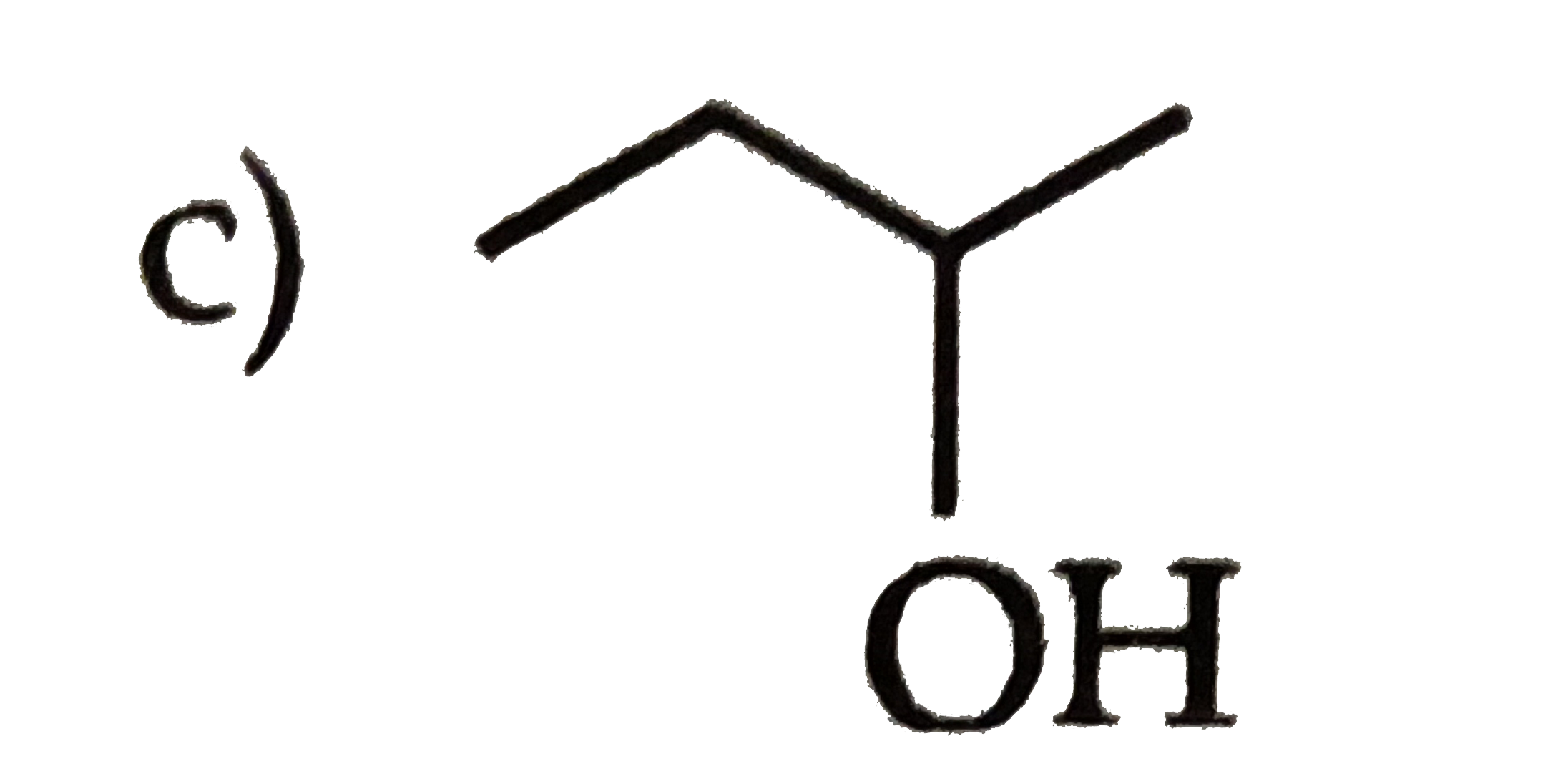 D
D