The correct Answer is:a→r,b→s,c→p,d→q.
a. cos22x−sin2x=0
⇒cos3xcosx=0
⇒cos3x=0orcosx=0
⇒3x=(2n−1)π2orx=(2n−1)π2,n∈Z
or x=(2n−1)π6orx=(2n−1)π2
Hence, the general solution is (2n−1)π6 as (2n−1)π2 is
contained in (2n−1)π6.
b. cosx+√3sinx=√3
or cosx2+√32sinx=√32
or cos(x−π3)=cosπ6
⇒x−π3=2nπ±π6,n∈Z
⇒x=2nπ+π2orx=2nπ+π6
c. √3tan2x−(√3+1)tanx+1=0
or √3tanx(tanx−1)−(tanx−1)=0
or (tanx−1)(√3tanx−1)=0
∴tanx=1⇒x=nπ+π4,n∈Z
or tanx=1√3⇒x=nπ+π6,n∈Z
d. tan3x−tan2x−tanx=0
or tanxtan2xtan3x=0
x=nπornπ/2 (rejected) or nπ/3
Therefore, the general solution is nπ/3 as nπ is contained in nπ/3.
Topper's Solved these Questions
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGECHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Exercise (Numerical)
21 Videos
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGECHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - JEE Main Previous Year
2 Videos
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGECHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Exercise (Comprehension)
20 Videos
- TRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONSBOOK - CENGAGECHAPTER - TRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONSEXERCISE - Question Bank
34 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGECHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - SINGLE CORRECT ANSWER TYPE
38 Videos
Similar Questions
Number of values of p for which equation sin3x+1+p3−3ψnx=0(p>) has a root is ________
View SolutionIf 0≤x≤2π, then the number of real values of x, which satisfy the equation cosx+cos2x+cos3x+cos4x=0, is
View SolutionCosider the cubic equation : x3−(1+cosθ+sinθ)x2+(cosθsinθ+cosθ+sinθ)x−sinθcosθ=0 whose roots are x1,x2,x3. The value of (x1)2+(x2)2+(x3)2 equals
View SolutionNumber of solutions of the equation
sin7θ=sinθ+sin3θ∈0<θ<π2 is equal to
View SolutionThe circular wire of diameter 10 cm is cut and placed along the circumference of a circle of diameter 1 meter. The angle subtended by the wire at the centre of circle is equal to
View SolutionHow many lines of symmetry does the above figure have ?
View SolutionWhich of the following are correct chain isomers of butane ? (i)
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionDtermine the images of the following figure about the given line :
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionFind the area of the figure given below.
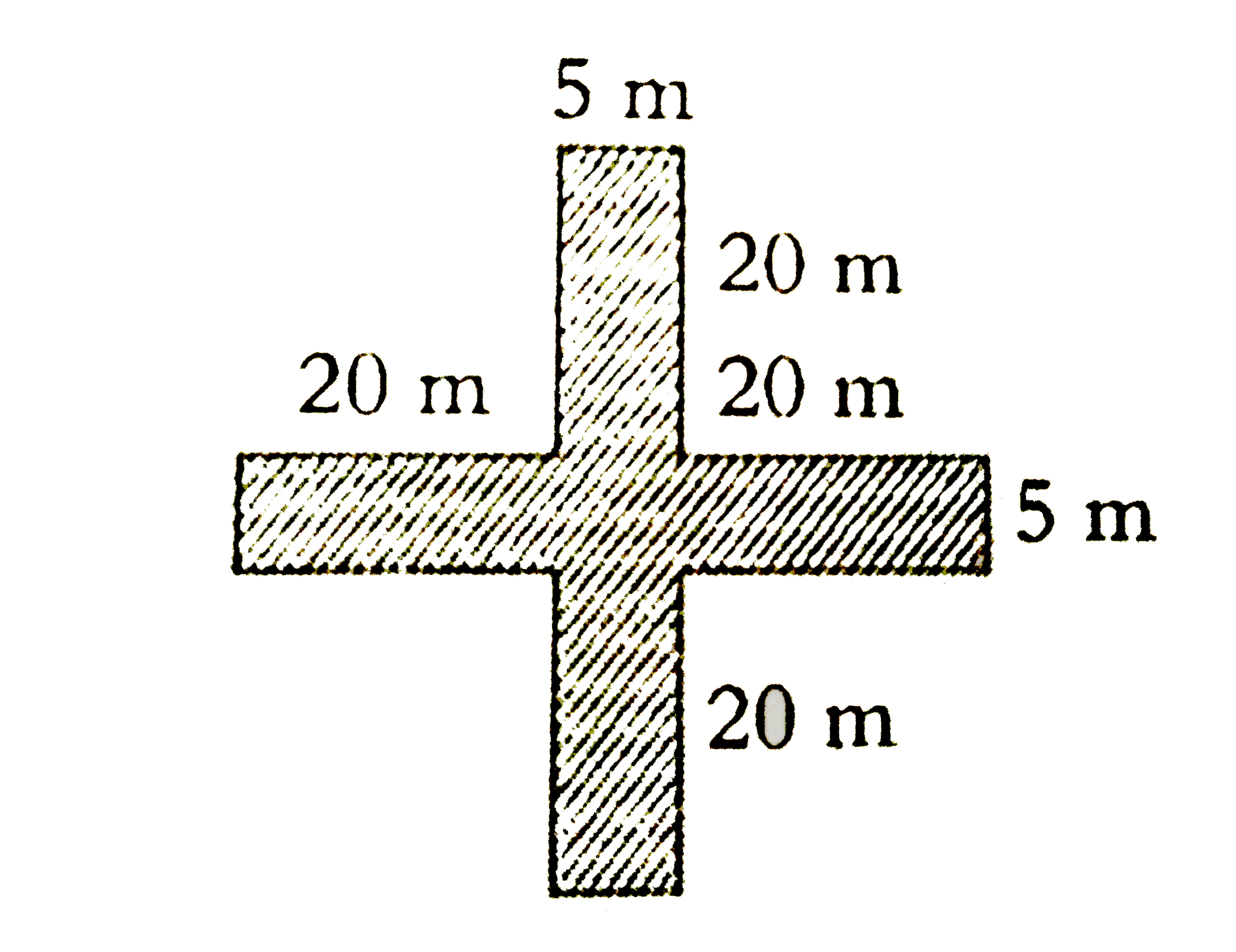
View SolutionThe area of the shaded part in the figure given below is ______.
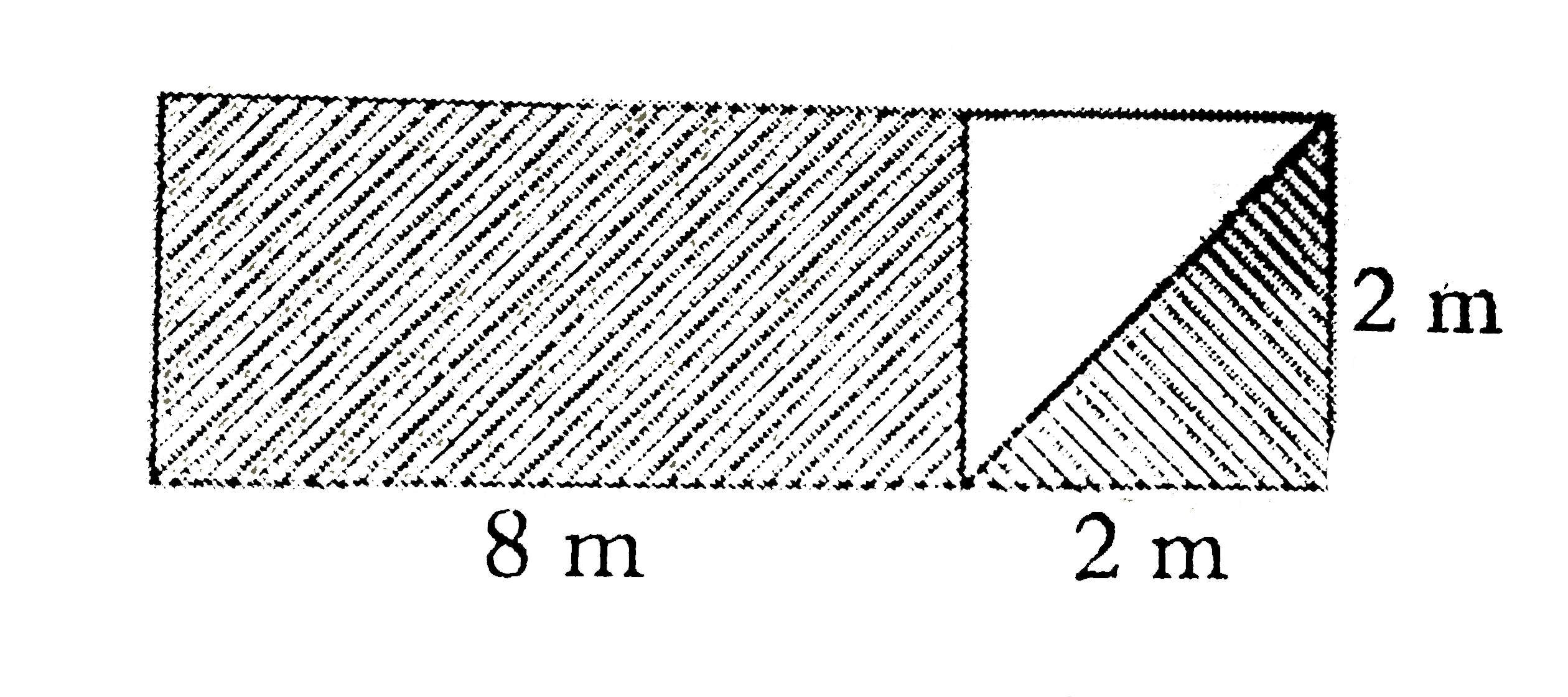
View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View Solution

