Question

Let $x^2-(m-3)x+m=0(m\in$ R) be a quadratic equation. Find the value of m for which the roots are
(i) real and distinct
(ii) equal
(iii) not real
(iv) oppsite in sing
(v) equal in magnitude but opposite in sing
(vi) positive
(vii) negative
(viii) such that at least one is positive
(ix) one root is smaller than 2 and the other root is greater then 2
(x) both the roots are grater then 2
(xi) both the roots are smaller then 2
(xii) exactly one root lies in the interval ( 1, 2)
(xiii) both the roots lie in the interval (1, 2)
(xvi) at least one root lies in the interval (1, 2)
(xv) one root is greater than 2 and the other root is smaller than 1

Explanation

Let `f(x) = x^(2) - m ( m - 3) x + m = 0`
(i) Both the roots are real and distinct. So, `D gt`0
`rArr (m - 3)^(2) - 4m gt ` 0
or `m^(2) - 10m + 9 gt`0
or `(m -1) (m - 9) gt` 0
`rArr m in (-infty, 1 ) cup (9, infty)`

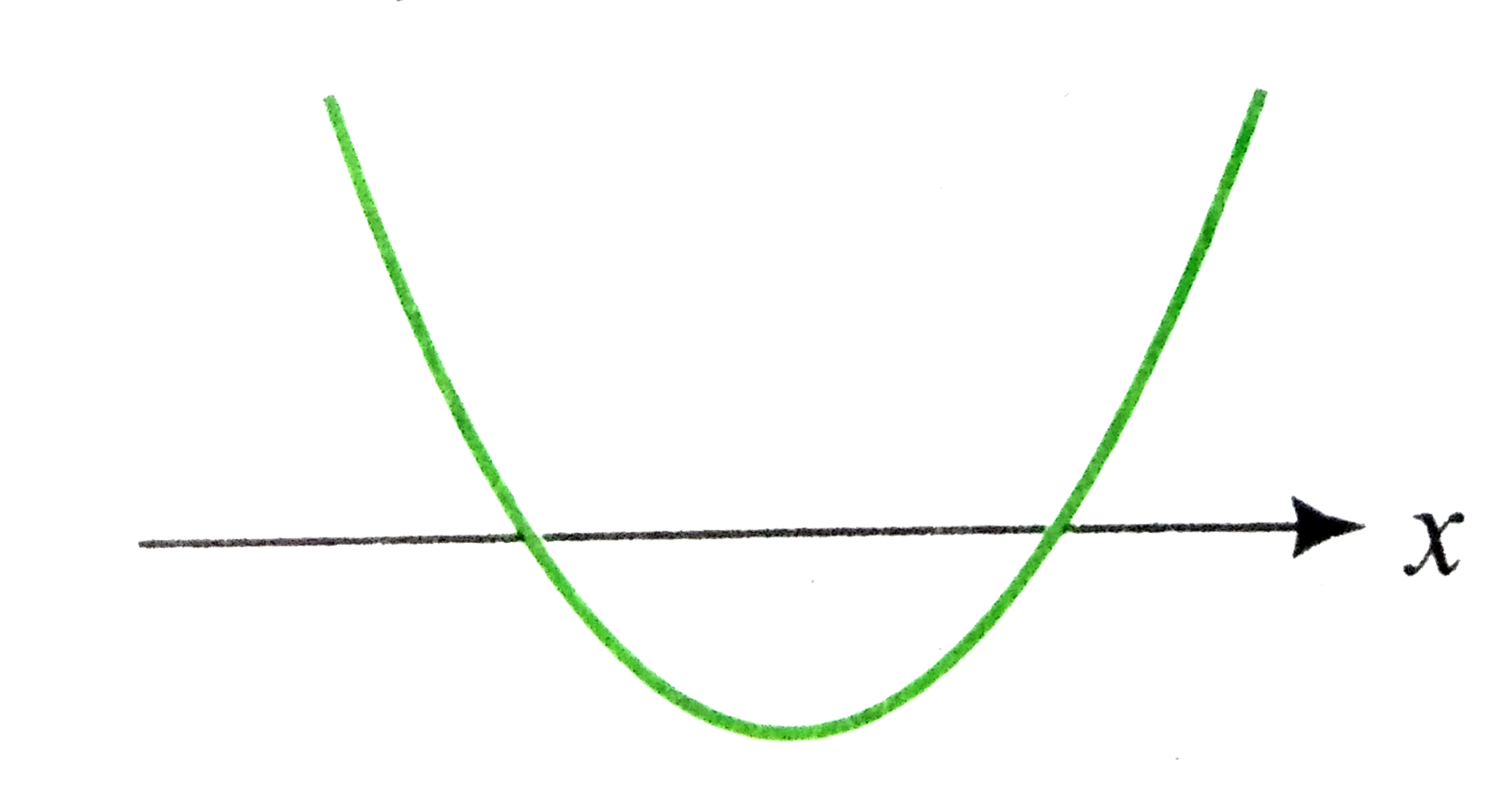
(ii) Both the roots are equal. So
`D= 0`
`rArr m = 9 or m = 1`

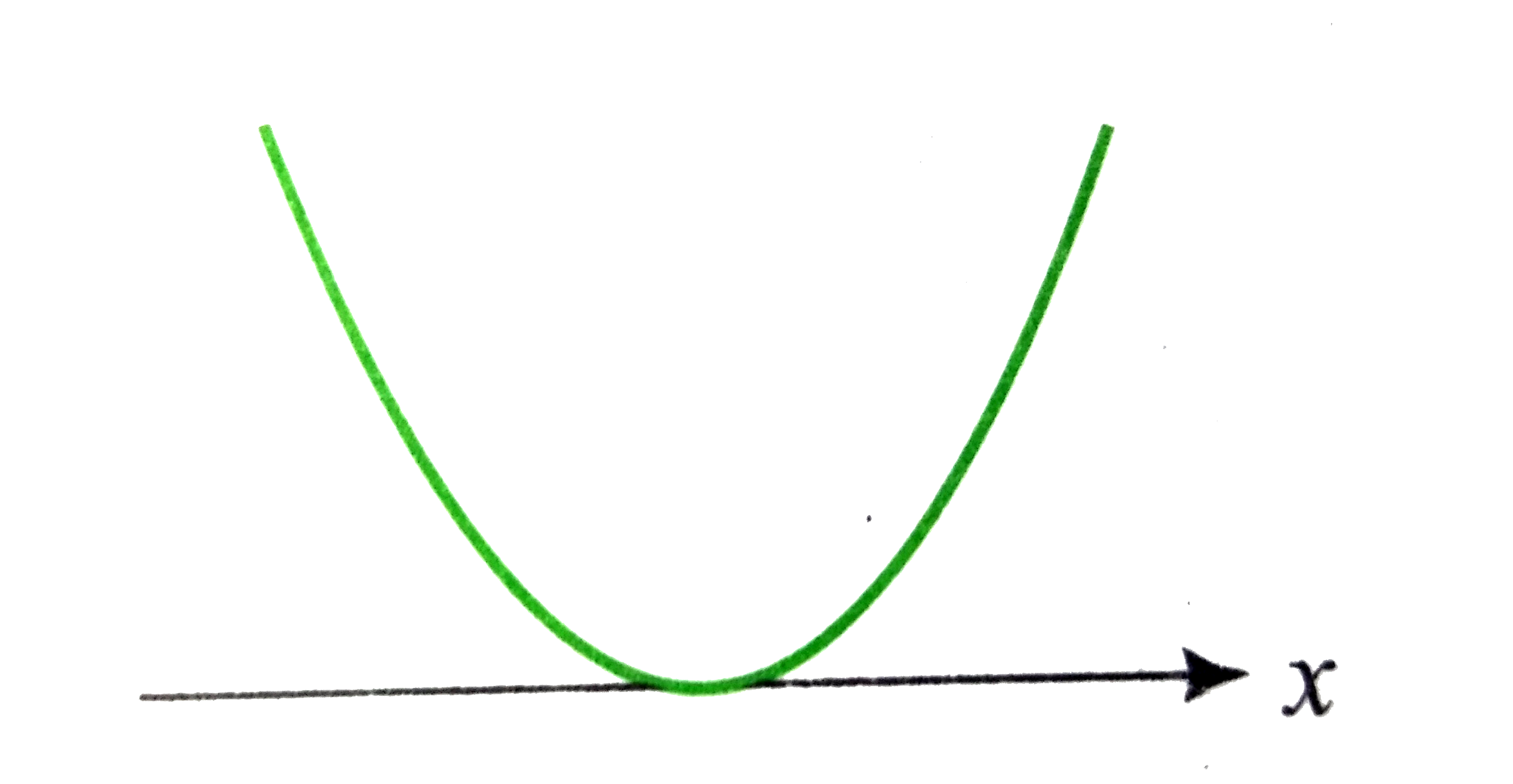
(iii) Both the roots are imaginary. So,
`D lt`0
`rArr ( m - 1) (m - 9) lt` 0
`rArr m in` ( 1, 9)

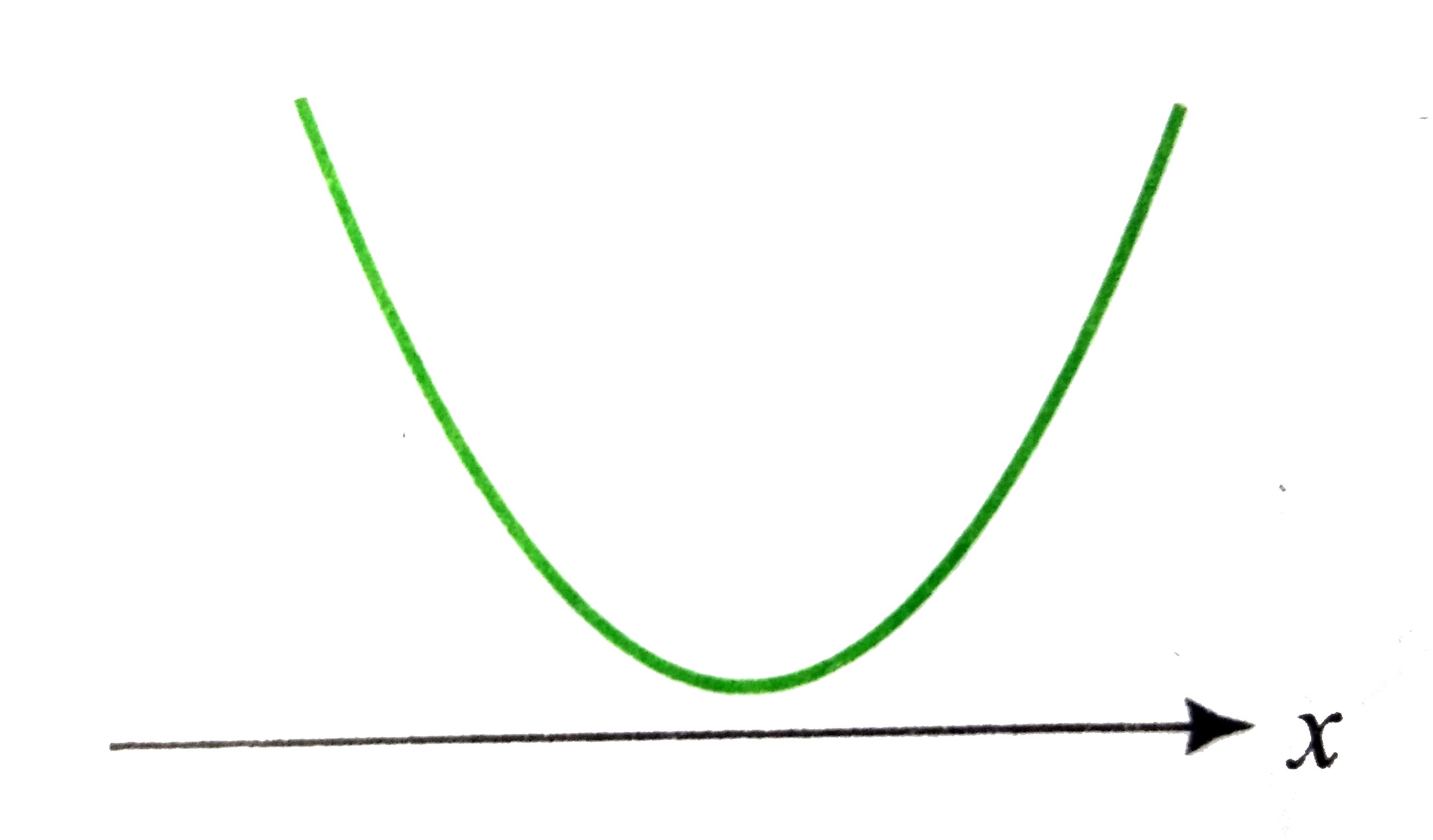
(iv) The roots are oppsite in sing . Hence, the product of root is negative. So,
`m lt rArr m in (-infty, 0)`

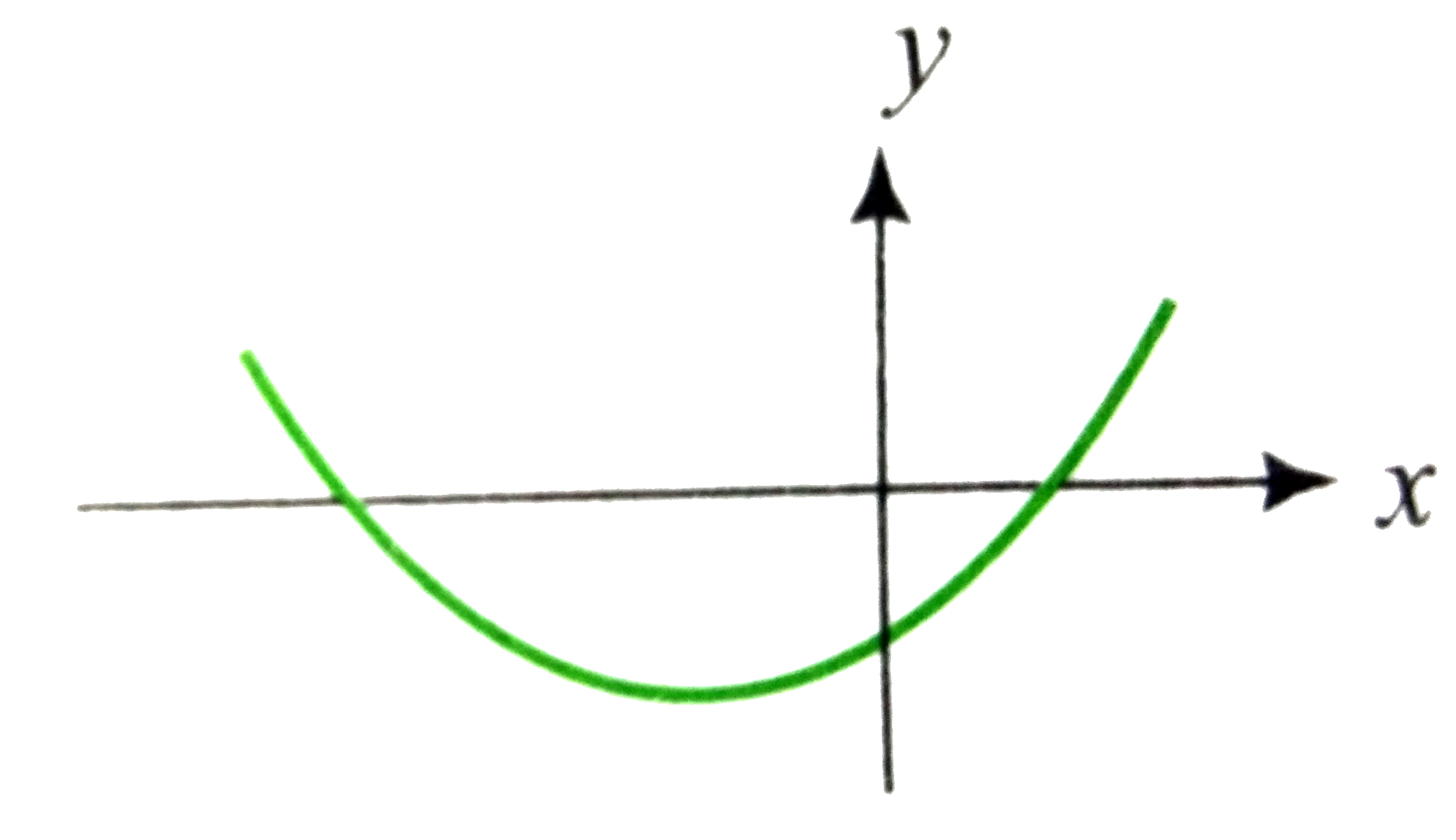
(v) Roots are equal in magnitude but opposite in sign . Hence, sum of roots is zero as well as D`ge 0. ` So,
m `in (-infty, 1) cup (9, infty)`
and `m - 3 = 0, i.e., m = 3`
Hence, so such m exists.

(vi)
Both the roots are positive. Hence, `D lt ` 0, and both the sum and the product of roots are positive. So,
m - 3`gt 0, m gt` 0 and m `(-infty, 1] cup [9, infty)`
m `in [ 9, infty)`
(vii)
At least one root is positive . Hence, either one root is positive or both roots are positive . So,
m`in (-infty, 0) cup [9, infty)`
(ix)
One root is smaller then 2 and the other root is greater than 2, i.e., 2 lies between the roots. So,
`f(2) lt` 0
`rArr 4 -2 (m - 3) + m lt` 0
`rArr m gt ` 10
(x)
Both the roots are greater then 2. So,
`f(2) gt 0, D ge 0, - (b)/(2a) gt` 2
`rArr m lt` 10 and m `in ( - infty, 1] cup [9, infty)` and m - 3 `gt`4
`rArr m in` [ 9, 10)
(xi)
Both the roots are smaller then 2. So,
`f(2) gt 0, ge 0, - (b)/(2a) lt` 2
`rArr m in (-infty, 1]`
Exactly one root lies in (1, 2) . So,
`f(1) f(2) lt` 0
`rArr 4(10 - m ) lt` 0
`rArr m in (10, infty)`
(xiii) Both the roots lie in the interval (1, 2) . Then,
D `ge 0 rArr (m - 1) (m - 9) ge` 0
`rArr m le 1 or ge `9 (1)
Also `f(1) gt `0 and `f(2) gt 0 rArr 10 lt ` m (2)
and `1lt-(b)/(2a) lt 2 rArr 5 lt m lt 7` (3)
Thus, no such m exists.
(xvi) Cace I : Exactly one root lies in (1, 2 ). So,
`f(1)f(2) lt 0 rArr m gt `10
Case II: Both the roots lie in (1, 2). S0, from (xiii),
m `in phi`. Hence, m `in (10, infty`).
For one root greater than 2 and the other root smaller than 1,
`f(1)lt` 0 and `f(2) lt` 0
But `f(1) = 4. Thus, no such m exists.