Find the value of a if x3−3x+a=0 has three distinct real roots.
Video Solution
Text Solution
The correct Answer is:−2<a<2
Let f(x)=x3−3x=a
Let f'(x)=0
⇒3x2−3=0orx=±1
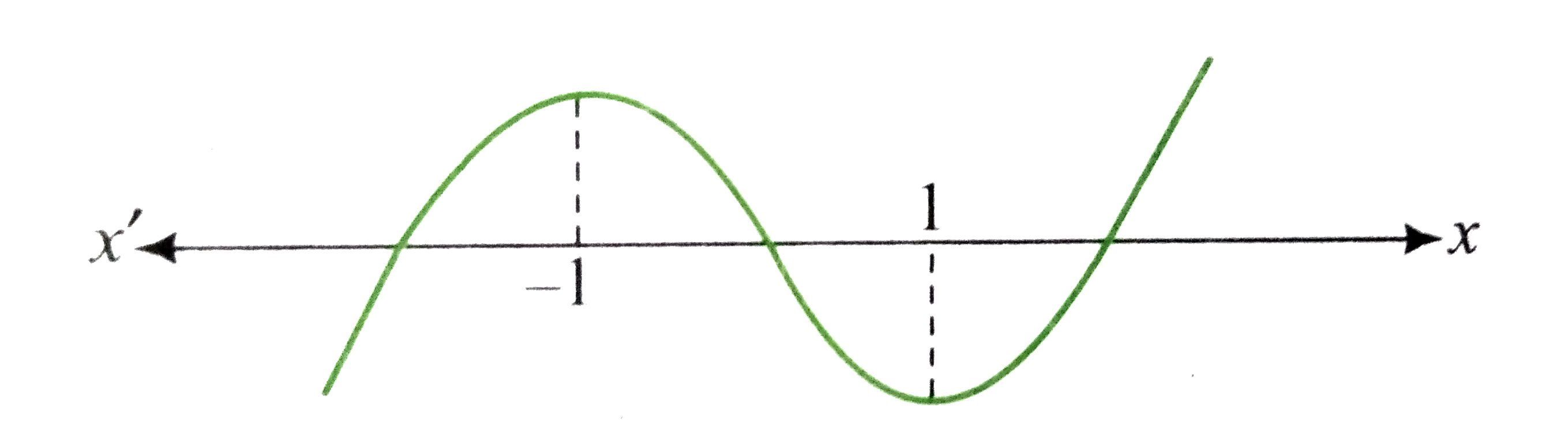
For three distinct roots , f(1)<0andf(−1)>0
⇒1−3+a<0and−1+3+a>a
or a<2anda>−2
or −2<a<2
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise 2.79videos
THEORY OF EQUATIONS
- BOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise 2.811videos
THEORY OF EQUATIONS
- BOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise 2.54videos
THEORY OF EQUATIONS
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - JEE Advanced Previous Year4videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - Question Bank20videos
THREE DIMENSIONAL GEOMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One
The real number k for which the equation 2x3+3x+k=0 has two distinct real roots in [0, 1]
Alies between 1 and 2Blies between 2 and 3Clies between -1 and 0Ddoes not exist - Question 2 - Select One
Suppose the cubic x3−px+q has three distinct real roots, where p>0 and q>0. Then which one of the following holds?
AThe cubic has maxima at both √p3 and −√p3BThe cubic has minima at √p3 and maxima at −√p3CThe cubic has minima st −√p3 and maxima at √p3DThe cubic has minima at both √p3 and −√p3 - Question 3 - Select One
The set of all positive real values of k, for which the equation x3−9x2+24x−k=0 has three distinct real roots, is the interval :
A(18, 21)B(16,20)C(14,18)D12, 16)
Find the values of k for which the equation x2−4x+k=0 has distinct real roots.
View SolutionFind a for which x2+(a−b)x+(1−a−b)= has two distinct real roots for ∀b∈R
View SolutionIf the equation 2x3−6x+k=0 has three real and distinct roots, then find the value (s) of k.
View SolutionFind the values of k for which the given equation has real roots: 9x2+3kx+4=0
View Solutionif the quadratic equation is 3x2+2x−1=0. then positive value of x is
View Solution
