Doubtnut Promotions Sticky

if the roots of the quadratic equation (4p−p2−5)x2 −2mx+m2−1=0 are greater then - 2 less then 4 lie in the interval

A

1

B

2

C

3

D

4

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:2

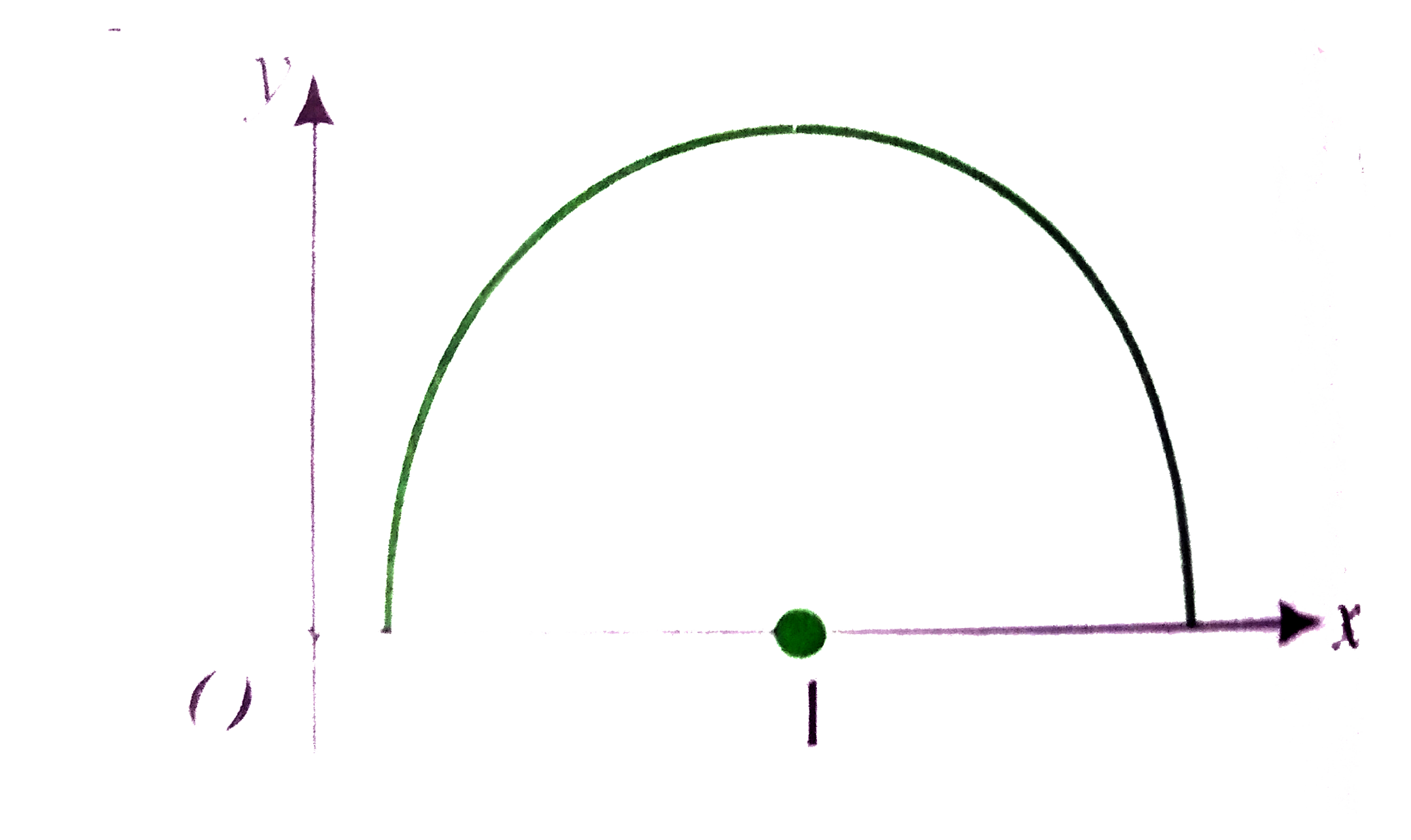
Note that coefficient of x2is(4p−p2−5)<0 . Therefore, the
graph is concave downward . According to the question , I must
lie between the roots . Hence,
f(1)>0
⇒4p−p2−5−2p+13p>0 lt brgt ⇒−p2+5p−4>0
⇒p2−5p+4<0
⇒(p−4)(p−1)<0
⇒1<p<4
⇒p∈{2,3}
ocr_image

|
Updated on:21/07/2023
Class 12MATHSQUADRATIC EQUATIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    The number of real roots of the quadratic equation (x−4)2+(x−5)2+(x−6)2=0 is

    A1
    B2
    C3
    DNone of these
  • Question 2 - Select One

    If p∈(−1,1) , then roots of the quadratic equation (p−1)x2+px+√1−p2=0 are

    Apurely imaginary
    Bnon-real complex combers
    Creal and equal
    Dreal and distinct
  • Question 3 - Select One

    If both the roots of the quadratic equation x2−mx+4=0 are real and distinct and they lie in the interval [1, 5], then m lies in the interval

    A(4, 5]
    B(3, 4)
    C(5, 6)
    D(−5,−4)