$a x^{2} + b x + c = 0 (a > 0),$ has two roots $α and β$ such $α < - 2 and β > 2,$ then

A

$a - | b | + c < 0$

B

$c < 0, b^{2} - 4 a c > 0$

C

$4 a - 2 | b | + c < 0$

D

$9 a - 3 | b | + c < 0$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:1,2,3

$f (x) = a x^{2} + b x + c$
$f (0) = c < 0, D > 0$
$\Rightarrow b^{2} - 4 a c > 0$
$f (1) < 0 and f (- 1) < 0$
$\Rightarrow a - | b | + c < 0$
$f (2) < 0 and f (- 2) < 0$
$\Rightarrow 4 a - 2 | b | + c < 0$

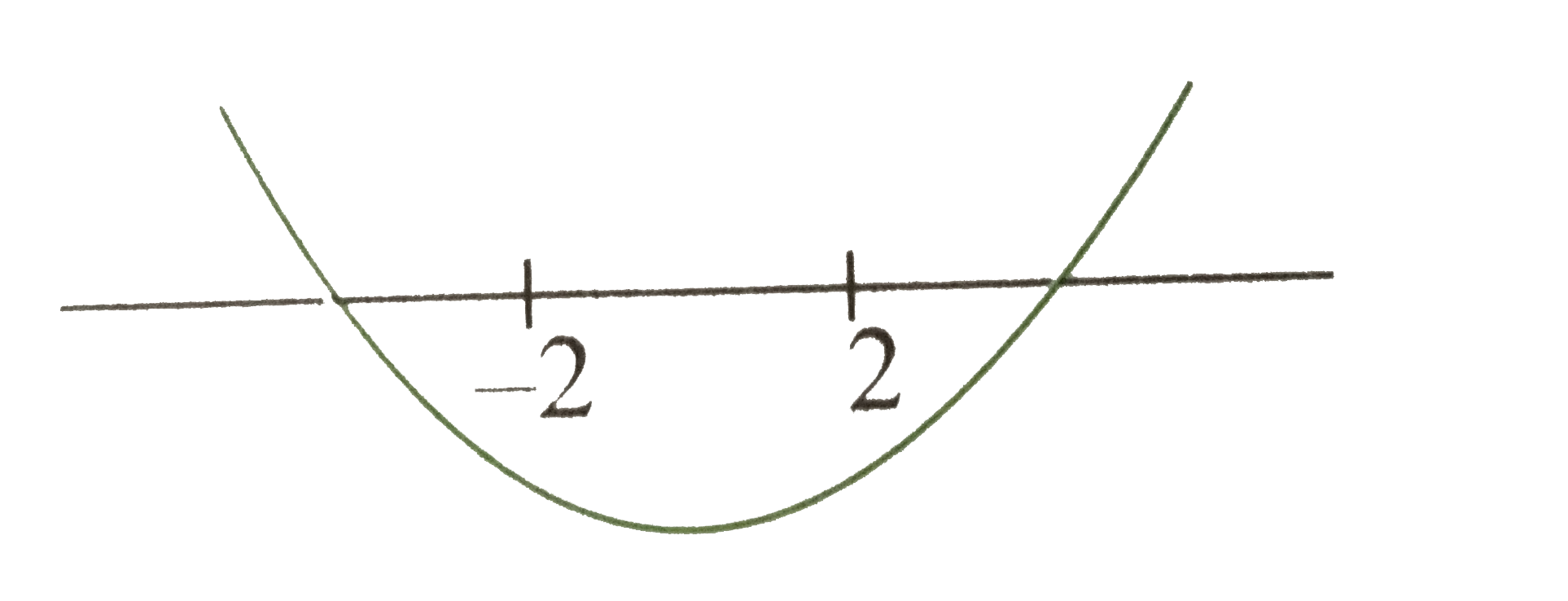
Nothing can be said about $f (3) or f (- 3)$ , whether it is positive
or negative .

|

Updated on:21/07/2023

Class 12 MATHS QUADRATIC EQUATIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
If the equation $a x^{2} + b x + c = 0 (a > 0)$ has two roots $α and β$ such that $α < - 2 and β > 2$ , then
A $b^{2} - 4 a c > 0$
B $4 a + 2 | b | + c < 0$
C $a + | b | + c < 0$
D $c < 0$
Question 2 - Select One
If the equation $a x^{2} + b x + c = 0 (a < 0)$ has two roots $α$ and $β$ such that $α < - 3$ and $β > 3$ , then
A $4 a - 2 | b | + c < 0$
B $9 a - 3 | b | + c < 0$
C $a - | b | + c < 0$
D $c < 0, b^{2} - 4 a c > 0$
Question 3 - Select One
If $α$ and $β$ are the roots of the equation $a x^{2} + b x + c = 0$ , and $p x^{2} + q x + r = 0$ has roots $\frac{1 - α}{α}$ and $\frac{1 - β}{β}$ , then r is equal to
Aa+2b
Ba+b+c
Cab+bc+ca
Dabc

CENGAGE-THEORY OF EQUATIONS-Exercise (Multiple)

Home
Ask Doubt
Profile