Consider equation ((x2+x)2)+a(x2+x)+4=0 Match the values of a in Lits II for the types of roods in Lits I.
abcd(1)pqrs
abcd(2)qrrp
abcd(3)rpsq
abcd(4)qspr
The correct Answer is:1
(x2+x)2+a(x2+x)+4=0
Let t=x2+x=(x+1/2)2−1/4.
⇒t∈[−14,∞]
Now, f(t)=t2+at+4=0 ....(1)
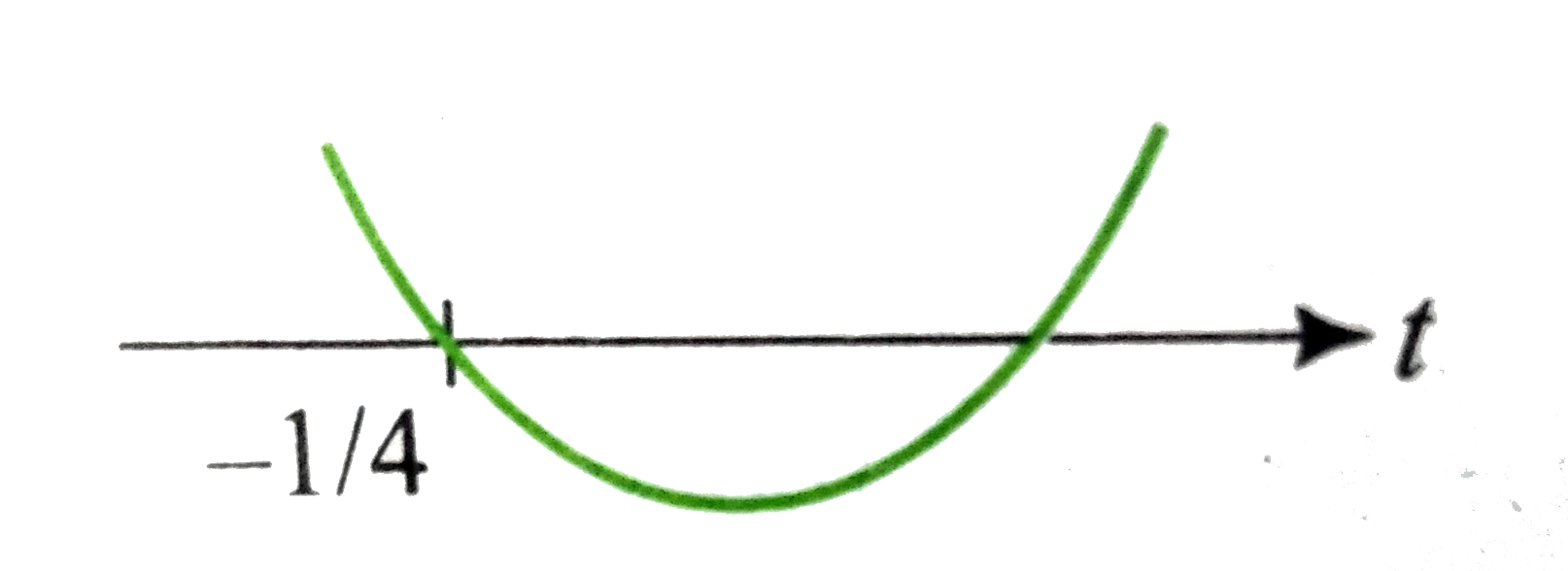
(a) All four real and distinct roots.
So, equation (1) has both roots greater then −1/4.

Following conditions are required:
(i)D>0⇒a2−16>0⇒|a|>4
(ii) f(−1/4)=116−a4+4>0⇒a<65/4
(iii) −B2A=a2>−14⇒a<12
⇒a∈(−∞,−4)
(b) Two real roots which are distinct.

⇒f(−1/4)<0
⇒a>65/4
⇒a∈(65/4,∞)
(c) All four roots are imaginary.
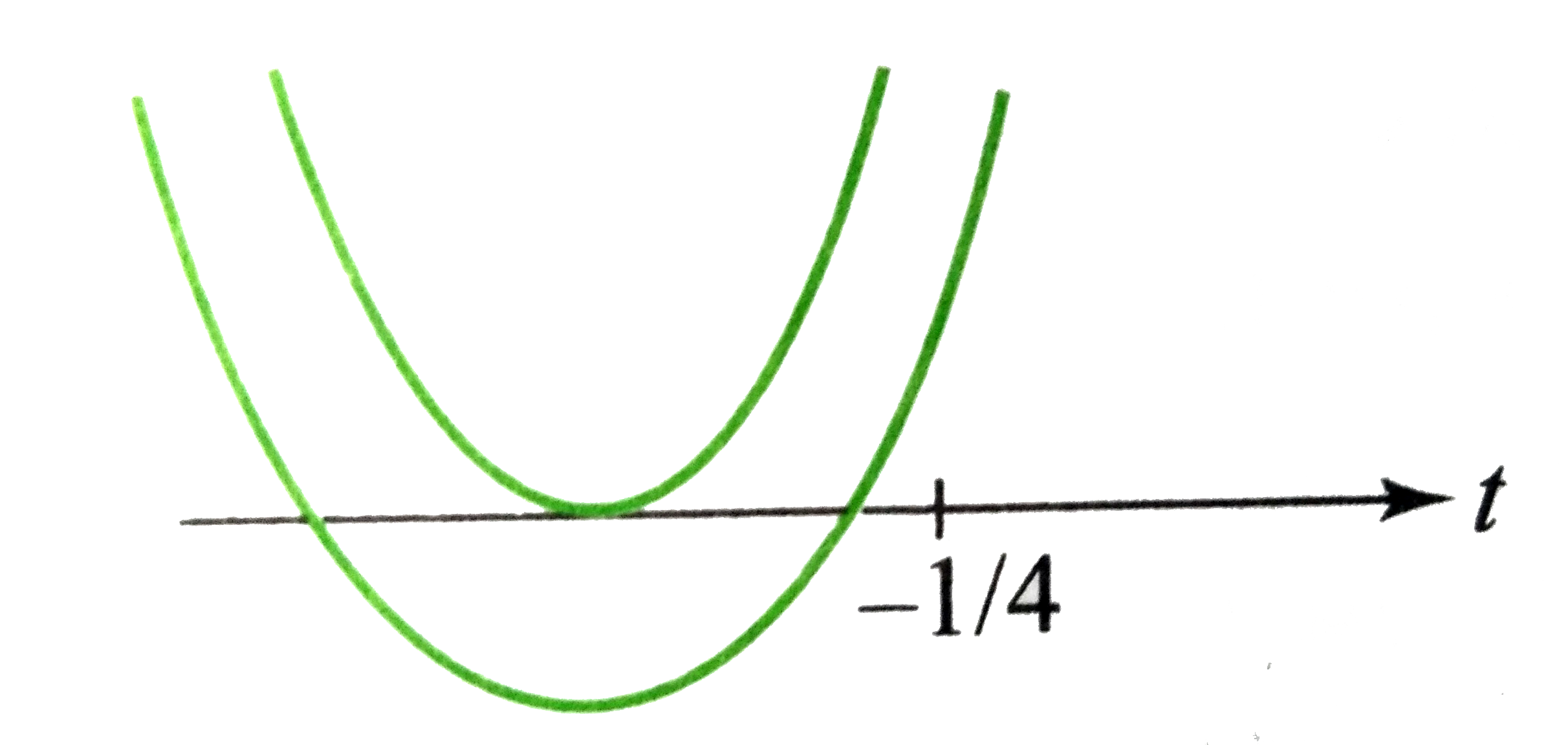
(i) D≥0⇒|a|≥4
(ii) f(−1/4)>0⇒a<654
(iii) −B2A<−14⇒a>12⇒a∈[4,654]
Case II:
D<0
⇒a∈(−4,4) ....(2)
From case I and case II,
a∈(−4,654)
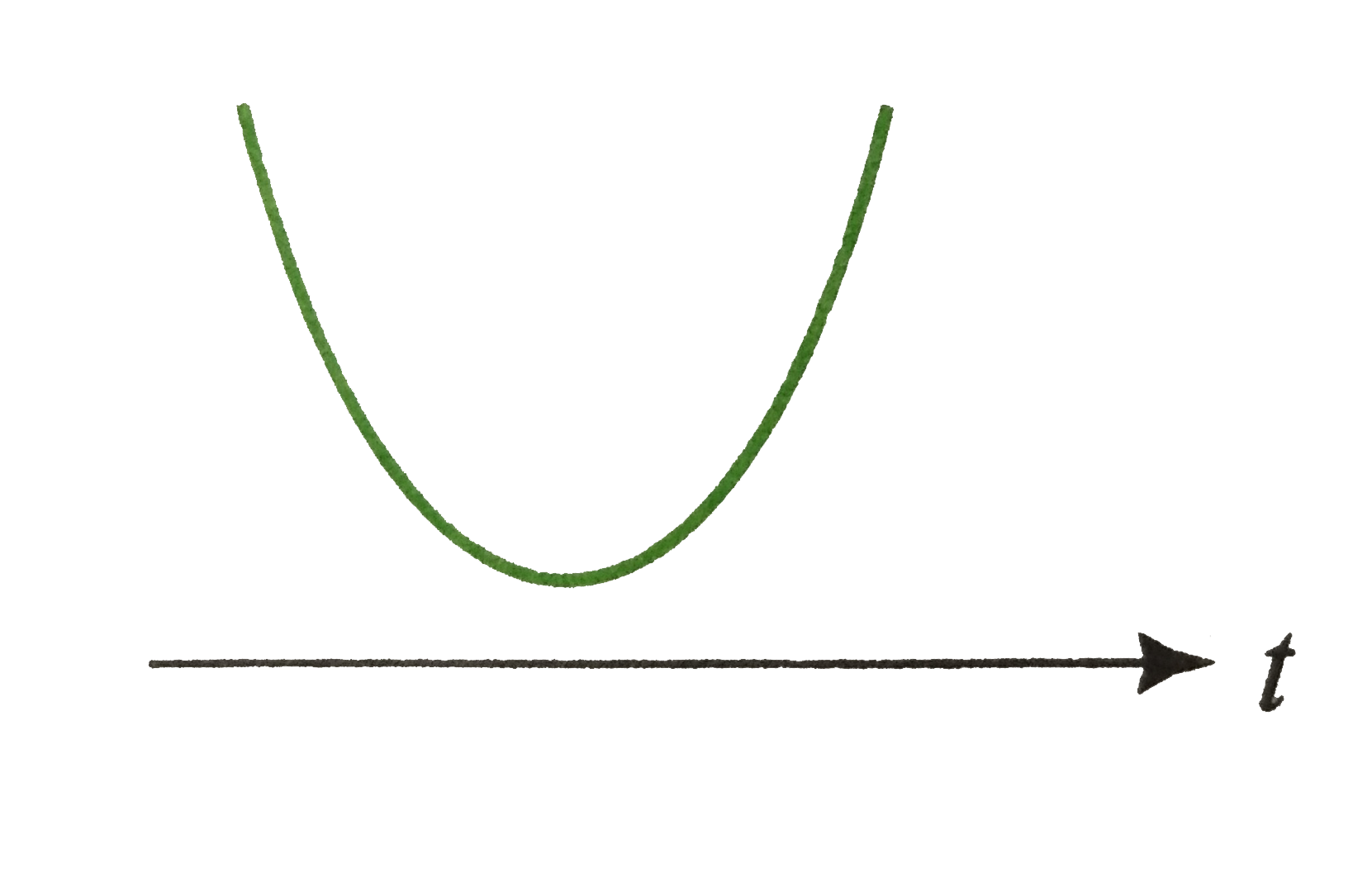
(d) Four real roots in which two are equal.
(i) D>0⇒|a|>4
(ii) f(−1/4)=0⇒a=65/4
(iii) −B2A>−14⇒a<12
No common solution.
∴a∈ϕ.
Topper's Solved these Questions
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Numerical)
43 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Main Previous Year
7 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Comprehension)
37 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - JEE Advanced Previous Year
4 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGECHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - Question Bank
20 Videos
Similar Questions
Knowledge Check
Consider equation x4−6x3+8x2+4ax−4a2=0,a∈R. Then match the following lists:
 Aabcd(1)qssrBabcd(2)rsqpCabcd(3)qsrpDabcd(4)qrpp
Aabcd(1)qssrBabcd(2)rsqpCabcd(3)qsrpDabcd(4)qrppConsider the equation log22x−4log2x−m2−2m−13=0,m∈R. Let the real roots of the equation be x1,x2 such that x1<x2.
The sum of maximum value of, x1 and minimum value of x2 is :A5138B5134C10258D2574If the equation x^4 -λx^2 +9 has only two real roods, then the set of values of λ is
A(−∞,−6)B(−6,6)C{6}Dϕ
Consider the equation log22x−4log2x−m2−2m−13=0,m∈R. Let the real roots of the equation be x1,x2 such that x1<x2.
The sum of maximum value of, x1 and minimum value of x2 is :
View SolutionIf the equation x^4 -λx^2 +9 has only two real roods, then the set of values of λ is
View Solutionconsider the ellipse x2+2y2−4x−4y+4=0 and match column I to column II according to the given condition.

View SolutionConsider the equation x4+x2+1=0 .If x1,x2,x3,x4 are roots of this equation, then the value of x61+x62+x63+x64 is equal to
View SolutionConsider the equation (log2x)2−4log2x−m2−2m−13=0,m∈R . Let the real roots the equation be x1,x2 such that x1<x2 .
The sum of maximum value of x1 and minimum value of x2 is :
View Solution
