If complex number z=x +iy satisfies the equation $R e (z + 1) = | z - 1 |$ , then prove that z lies on $y^{2} = 4 x$ .

Video Solution

Text Solution

Verified by Experts

We have $R e (z + 1) = | z - 1 |$
$\Rightarrow R e (x + i y + 1) = | x + i y - 1 |$
$\Rightarrow x + 1 = \sqrt{{(x - 1)}^{2} + y^{2}})$
$\Rightarrow {(x + 1)}^{2} = {(x + 1)}^{2} + y^{2}$
$\Rightarrow y^{2} = 4 x$
Thus, z lies on $y^{2} = 4 x$ .

|

Updated on:21/07/2023

Class 12 MATHS COMPLEX NUMBERS

Topper's Solved these Questions

BOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Exercise 3.1
4videos
COMPLEX NUMBERS
BOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Exercise 3.2
9videos
COMPLEX NUMBERS
BOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Comprehension
11videos
COMPLEX NUMBERS
BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
32videos
CIRCLES
BOOK - CENGAGECHAPTER - CONIC SECTIONSEXERCISE - Solved Examples And Exercises
91videos
CONIC SECTIONS

Similar Questions

Knowledge Check

Question 1 - Select One
The complex number z =x+iy which satisfies the equation $∣ ∣ ∣ \frac{z - 3 i}{z + 3 i} ∣ ∣ ∣ = 1,$ then on
Athe X-axis
Bthe straight line y = 3
Ca circle passing through origin
DNone of the above
Question 2 - Select One
The complex number z =x+iy which satisfies the equation $∣ ∣ ∣ \frac{z - 3 i}{z + 3 i} ∣ ∣ ∣ = 1,$ then on
Athe X-axis
Bthe straight line y = 3
Ca circle passing through origin
DNone of the above
Question 3 - Select One
The complex numbers z = x + iy which satisfy the equation $∣ ∣ ∣ \frac{z - 5 i}{z + 5 i} ∣ ∣ ∣ = 1$ , lie on

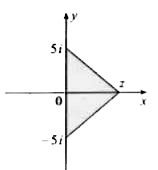Athe x - axis
Bthe straight line y = 5
Ca circle passing through origin
DNone of these

CENGAGE-COMPLEX NUMBERS-Examples

Home
Ask Doubt
Profile