Find the time required for a cylindrical tank of radius r and height H to empty through a round hole of area a at the bottom. The flow through the hole is according to the law v(t)=k√2gh(t) , where v(t) and h(t) , are respectively, the velocity of flow through the hole and the height of the water level above the hole at time t, and g is the acceleration due to gravity.

Let at time t the depth of water is h and radius of water surface is r. If in time dt the decrease of water level is dh, then
−πr2dh=ak√2ghdt
or −πr2ak√2h√h=dt
or −πr2ak√2g=dh√h=dt
Now when t=0, h=H and when t=t, h=0, then
−πr2ak√2g∫0Hdh√h=∫t0dt
or −πr2ak√2g{2√h}0H=t
or t=πr22√Hak√2g=πr2ak√2Hg
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Exercise 10.16videos
DIFFERENTIAL EQUATIONS
- BOOK - CENGAGECHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Exercise 10.26videos
DIFFERENTIAL EQUATIONS
- BOOK - CENGAGECHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Exercise337videos
DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS
- BOOK - CENGAGECHAPTER - DIFFERENTIATIONEXERCISE - Numerical Value Type3videos
DIFFERENTIATION
Similar Questions
A hemi-spherical tank of radius 2 m is initially full of water and has an outlet of 12cm2 cross-sectional area at the bottom. The outlet is opened at some instant. The flow through the outlet is according to the law v(t)=√0.62gh(t), where v(t) and h(t) are, respectively, the velocity of the flow through the outlet and the height of water level above the outlet and the height of water level above the outlet at time t, and g is the acceleration due to gravity. Find the time it takes to empty the tank.
View SolutionFind the time required for a cylindrical tank of radius 2.5 m and height 3 m to empty through a round hole of 2.5 cm with a velocity 2.5√h m/s, h being the depth of the water in the tank.
View Solution
Knowledge Check
- Question 1 - Select One
A large tank filled with water to a height h is to be emptied through a small hole at the bottom. The ratio of times taken for the level of water to fall from h to h2 and from h2 to zero is
A√2B1√2C√2−1D1√2−1 - Question 2 - Select One
The contribution in the total current flowing through a semiconductor due to electrons and holes are 35 and 25 respectively. If the drift velocity of electrons is 2 times that of holes at this temperature, then the ratio of concentration of electrons and holes is
A5/2B6/5C5/3D3/4 - Question 3 - Select One
A large tank filled with water to a height h is to be emptied through a small hole at the bottom. The ratio of times taken for the level of water to fall from h to h2 and from h2 to zero is
A√2B12C√2−1D1√2−1
A vessel is filled with two different liquids of densities ρand2ρ respectively as shown in the figure. The velocity of flow of liquid through a hole at height h2 from bottom is
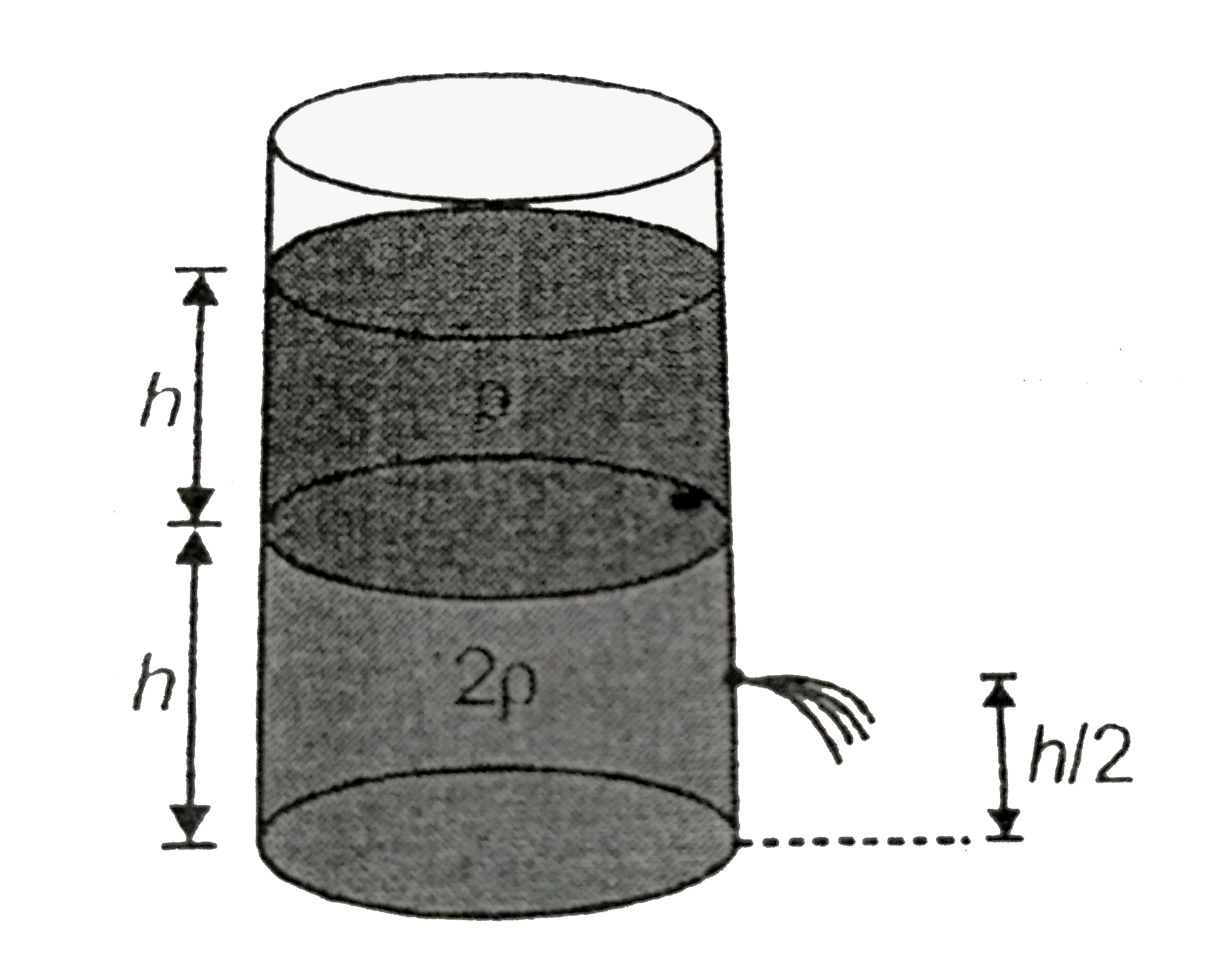 View Solution
View SolutionA particle is moving in a straight line according to the law S=t3+2t2+3t−4, where S is displacement and t is time. Find the velocity and acceleration when t=2.
View SolutionAssume a smooth hole drilled along the diameter of the earth. If a stone is dropped at one end it reaches the other end of the hole after a Time T0. Now instead of dropping the stone, you throw it into the hole with an initial velocity u. How big should u be, so that the stone appears at the other end of the hole after a time T02. Express your answer in terms of acceleration due to gravity on the surface of the earth (g) and the radius of the earth (R ).
View SolutionThe contribution in the total current flowing through a semiconductor due to electrons and holes are 34 and 14 respectively. If the drift velocity of electrons is 52 times that of holes at this temperature, then the ratio of concentration of electrons and holes is
View SolutionA body is projected veritclaly upwards.The times corresponding to height h while ascending and while descending are t1 and t2 respectively.
Then, the velocity of projection will be (take g as acceleration due to gravity)View Solution

