Three point charges +q, –2q and +q are placed at points (x = 0, y = a, z = 0), (x = 0,y = 0, z = 0) and (x = a, y = 0, z = 0) respectively. The magnitude and direction of the electric dipole moment vector of this charge assembly are:-
√2 qa along + x direction
√2 qa along + y direction
√2 qa along the line joining points (x=0,y=0,z=0) and (x=a,y=a,z=0)
qa along the line joining points (x=0,y=0,z=0) and (z=a , y=a ,z=0)
The correct Answer is:C
To find the electric dipole moment vector of the given charge assembly, we can follow these steps:
Step 1: Identify the positions and charges
We have three point charges:
- Charge +q at position (0,a,0)
- Charge −2q at position (0,0,0)
- Charge +q at position (a,0,0)
Step 2: Calculate the dipole moment contributions
The electric dipole moment →p for a system of point charges is given by the formula:
→p=∑qi→ri
where qi is the charge and →ri is the position vector of the charge.
Contribution from +q at (0,a,0):
→p1=+q⋅(0,a,0)=(0,qa,0)
Contribution from −2q at (0,0,0):
→p2=−2q⋅(0,0,0)=(0,0,0)
Contribution from +q at (a,0,0):
→p3=+q⋅(a,0,0)=(qa,0,0)
Step 3: Sum the contributions
Now, we sum the contributions from all three charges:
→p=→p1+→p2+→p3=(0,qa,0)+(0,0,0)+(qa,0,0)=(qa,qa,0)
Step 4: Write the dipole moment vector
Thus, the total electric dipole moment vector is:
→p=(qa,qa,0)=qa^i+qa^j
Step 5: Calculate the magnitude of the dipole moment
The magnitude of the dipole moment |→p| is given by:
|→p|=√(qa)2+(qa)2=√2(qa)2=qa√2
Step 6: Determine the direction of the dipole moment
The direction of the dipole moment vector →p can be expressed in terms of angles. Since both components are equal, the angle with respect to the axes can be determined using:
tanθ=pypx=qaqa=1⟹θ=45∘
Final Result
The magnitude of the electric dipole moment vector is qa√2 and the direction is at an angle of 45∘ from both the x-axis and y-axis.
We have three point charges:
- Charge +q at position (0,a,0)
- Charge −2q at position (0,0,0)
- Charge +q at position (a,0,0)
The electric dipole moment →p for a system of point charges is given by the formula:
→p=∑qi→ri
where qi is the charge and →ri is the position vector of the charge.
→p1=+q⋅(0,a,0)=(0,qa,0)
→p2=−2q⋅(0,0,0)=(0,0,0)
→p3=+q⋅(a,0,0)=(qa,0,0)
Now, we sum the contributions from all three charges:
→p=→p1+→p2+→p3=(0,qa,0)+(0,0,0)+(qa,0,0)=(qa,qa,0)
Thus, the total electric dipole moment vector is:
→p=(qa,qa,0)=qa^i+qa^j
The magnitude of the dipole moment |→p| is given by:
|→p|=√(qa)2+(qa)2=√2(qa)2=qa√2
The direction of the dipole moment vector →p can be expressed in terms of angles. Since both components are equal, the angle with respect to the axes can be determined using:
tanθ=pypx=qaqa=1⟹θ=45∘
The magnitude of the electric dipole moment vector is qa√2 and the direction is at an angle of 45∘ from both the x-axis and y-axis.
Topper's Solved these Questions
- NEETBOOK - NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE)CHAPTER - NEETEXERCISE - PHYSICS
157 Videos
- NEETBOOK - NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE)CHAPTER - NEETEXERCISE - QUESTION
95 Videos
- MOTION IN TWO AND THREE DIMENSIONBOOK - NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE)CHAPTER - MOTION IN TWO AND THREE DIMENSIONEXERCISE - All Questions
47 Videos
- NEET 2020BOOK - NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE)CHAPTER - NEET 2020EXERCISE - All Questions
45 Videos
Similar Questions
Two charges +q and -q are kept at (−x1,0)and(x1,0) respectively in the x-y plane. Find the magnitude and direction of the net electric field at the origin (0,0)
View Solution" Two point charges "+2q" and "-q" are placed on "x" -axis at "(0,0,0)" and "(3,0,0)" respectively,How many points of zero electric potential are there in the plane "X=5?
View Solution
Knowledge Check
The point charges +q,2q and +q are placed at point (x=0,y=a,z=0),(x=0,y=0,z=0) and (x=a,y=0,z=0), repectively. The magnitude and direction of the electric dipole moment vector of this charge assembly are
A√2qa along + y directionB√2qa along the line joining points
(x=0,y=0,z=0) and (x=a,y=a,z=0)Caq along the line joining points
(x=0,y=0,z=0) and (x=a,y=a,z=0)D√2qa along + x directionThree charged particles having charges q, -2q & q are placed in a line at points (-a, 0), (0,0) & (a , 0) respectively. The expression for electric potential at P(r, 0 ) for r >> a is
A14πε0qa2r4B14πε02qa2r3C14πε04qa2r2D14πε08qa2rThree charges -1, +q and +q are situated in x-y plane at points (0, -a)(0,0) and (0, a) respectively. The potential at a point distant r(r>a) in a direction making an angle θ from y - axis will be
AkqrBkqr2(2acosθ)Ckqr(1+2acosθr)Dkqa
Two charges - q and +q are located at points (0, 0, - a) and (0,0, a), respectively.
What is the electrostatic potential at the points (0, 0, z) and (x, y,0) ?
View SolutionAsserions: Two points charges +Q and −Q are fixed at point A(+a,0,0)and point B(−a,0,0) respectively.Then the magnitude of electric flux due to electric field of either point charge through infinite y-zplane (that is x=0 plane) is less than magnitude of net electric flux due to electric field of both charges through that plane (x=0 plane)
Reason :the magnitude of the net electric flux through a surface due to a system of point charges is equal to sum of magnitude of electric flux through that surface due to each of the point charge of the system.
View SolutionPoint charges +4q,−q and +4q are kept on the x-axis at points x=0,x=a and X=2a respectively, then
View SolutionFour charges +q,+q−q, and -q are placed on X - Y plane at the points whose coordinates are (0.5,0),(0,0.5),(−0.5,0)and(0,−0.5) respectively.
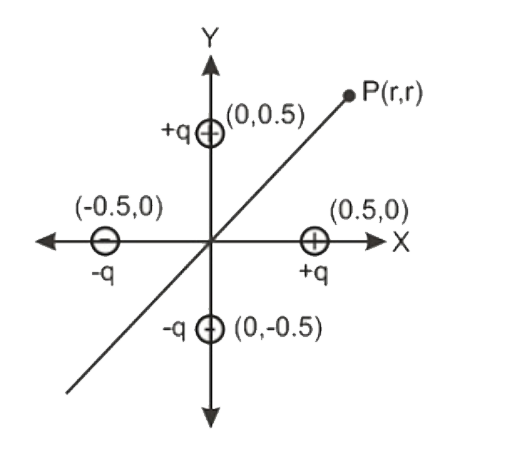
The electric field due to these charges at a point P(r,r), where r>>0.5, will be
View SolutionTwo point charges −q and +q are located at points (0,0−a) and (0,0,a) resepctively.The electric potential at point (0,0,z)is (Z>a)
View Solution
