If X=3−4t2+t3, then work done in first 4s. will be (Mass of the particle is 3 gram) :
384 mJ
168 mJ
192 mJ
None of these
The correct Answer is:A
Work energy theorem
W=ΔKE
x=3−4t2+t3
v=dxdt=−8t+3t2
v1(t=0)=0
v2(t=4)=16
Therefore,ΔKE=12mv22−12mv21
=12×3×10−3×16×16−0=384mJ
Topper's Solved these Questions
- NEETBOOK - NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE)CHAPTER - NEETEXERCISE - PHYSICS
157 Videos
- NEETBOOK - NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE)CHAPTER - NEETEXERCISE - QUESTION
95 Videos
- MOTION IN TWO AND THREE DIMENSIONBOOK - NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE)CHAPTER - MOTION IN TWO AND THREE DIMENSIONEXERCISE - All Questions
47 Videos
- NEET 2020BOOK - NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE)CHAPTER - NEET 2020EXERCISE - All Questions
45 Videos
Similar Questions
Knowledge Check
The position of a particle as a function of time is described by relation x=3t−3t2+t3, where the quantities are expressed in SI units. If mass of the particle be 10 kg, the work done in first three seconds is
A10 JB30 JC300 JD675 JThe position of a particle as a function of time is described by relation x=3t−3t2+t3 where the quantities are expressed in SI units. If mass of the particle be 10 kg, the work done in first three seconds is
A10 JB30 JC300 JD675 JThe position of a particle moving on a stringht line under rthe action of a force is given as x=50t−5t2 Here, x is in metre and t is in second. If mass of the particle is 2 kg, the work done by the force acting on the particle in first 5 s is.
A2500 JB−2500JC5000 JD−5000J
Acceleration of a paritcle moving in x−y plane varies with time t as. →a=(ti+3T2j).
Here a is in m/s2 and t in sec. At time t=0 particle is at rest origin. Mass of the particles is 1kg. Find the net work done on the particle in first 2sec.
View SolutionA force act on a 30gm particle in such a way that the position of the particle as a function of time is given by x=3t−4t2+t3, where x is in metros and t is in seconds. The work done during the first 4 second is
View SolutionThe displacement of a particle executing SHM is given by
Y=5 sin (4t+π3)
If T is the time period and the mass of the particle is 2g, the kinetic energy of the particle When t=T4 is given by-
View SolutionIf S=t33−2t2+3t+4, then
View SolutionIn the figure the variations of componets of acceleration of particles of mass 1kg is shown w.r.t. time. The initial velocity of the particle is →u=(−3ˆi+4ˆj)m/s. the total work done by the resultant force on the particles in time intervals from t=0 to t=4 seconds is :
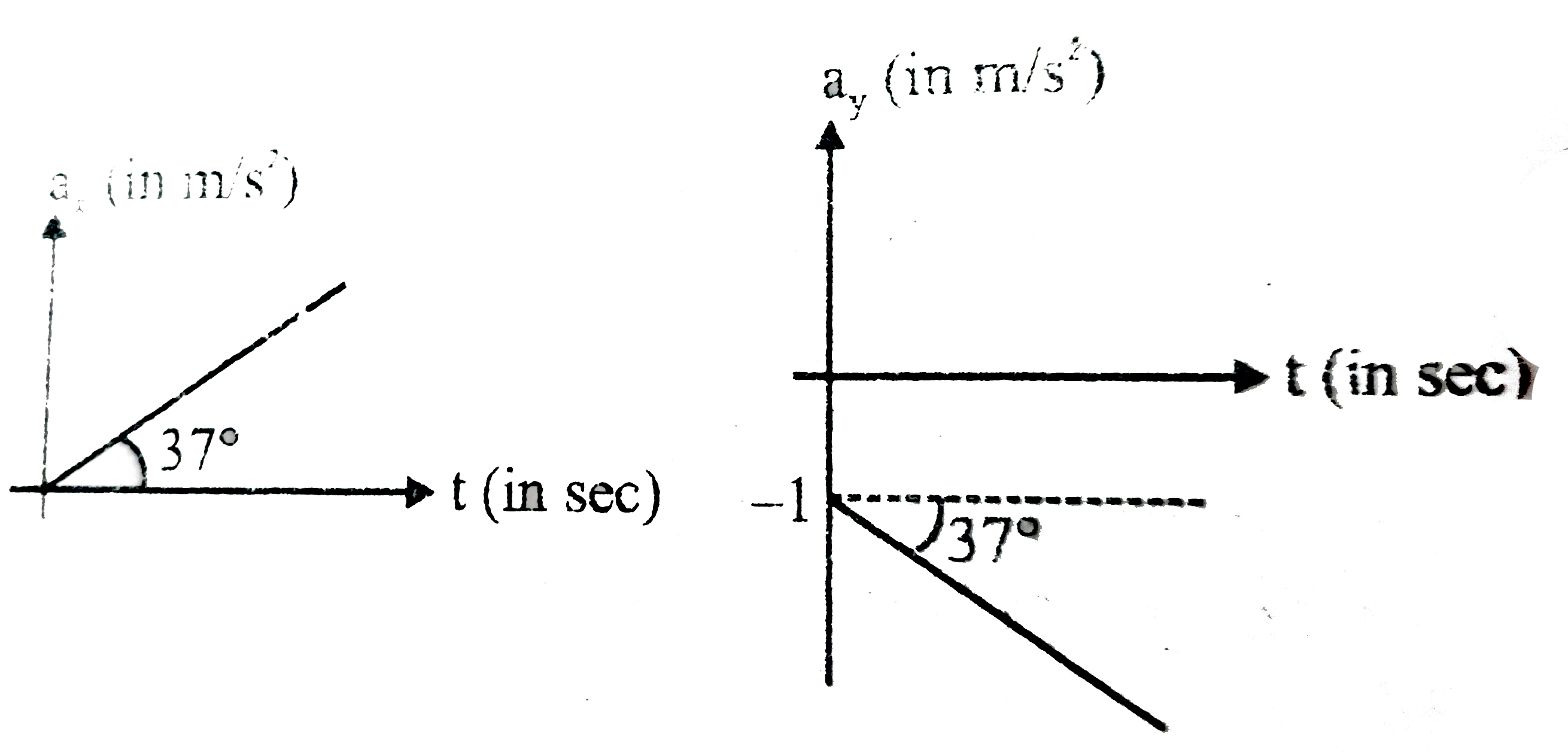
View Solution
