If spheres of radius 'r' are arranged in ccp fashion (ABC ABC…) the vertical distance between any two consecutive A layers is
4r√23
4r√32
6 r
r√6
To find the vertical distance between any two consecutive A layers in a cubic close-packed (CCP) arrangement, we can follow these steps:
Step 1: Understand the Arrangement
In a cubic close-packed (CCP) structure, the spheres are arranged in layers. The arrangement follows an ABCABC pattern, meaning that every third layer is identical.
Step 2: Identify the Relationship Between Radius and Edge Length
In a CCP structure, the spheres touch each other along the face diagonal. The relationship between the radius (r) of the spheres and the edge length (A) of the cube can be established. The face diagonal of the cube can be expressed as:
Face diagonal=√2A
Since the face diagonal also equals four times the radius (4r) of the spheres, we have:
4r=√2A
From this, we can derive the edge length (A):
A=4r√2=2√2r
Step 3: Calculate the Vertical Distance Between Layers
The vertical distance (H) between two consecutive A layers in the CCP structure can be calculated. The height of the unit cell (which contains the layers) is equal to the distance between the centers of the spheres in two consecutive layers.
In a CCP structure, the vertical distance between two layers is given by:
H=A√2
Substituting the expression for A we found earlier:
H=2√2r√2=2r
Step 4: Final Expression for Vertical Distance
Now, we need to express this vertical distance in terms of the radius (r). The distance between two consecutive layers can also be expressed in terms of the edge length (A) and the geometry of the arrangement:
H=2√2r√3=4r√3
Conclusion
Thus, the vertical distance between any two consecutive A layers in a cubic close-packed arrangement is:
H=4r√3
In a cubic close-packed (CCP) structure, the spheres are arranged in layers. The arrangement follows an ABCABC pattern, meaning that every third layer is identical.
In a CCP structure, the spheres touch each other along the face diagonal. The relationship between the radius (r) of the spheres and the edge length (A) of the cube can be established. The face diagonal of the cube can be expressed as:
Face diagonal=√2A
Since the face diagonal also equals four times the radius (4r) of the spheres, we have:
4r=√2A
From this, we can derive the edge length (A):
A=4r√2=2√2r
The vertical distance (H) between two consecutive A layers in the CCP structure can be calculated. The height of the unit cell (which contains the layers) is equal to the distance between the centers of the spheres in two consecutive layers.
H=A√2
Substituting the expression for A we found earlier:
H=2√2r√2=2r
Now, we need to express this vertical distance in terms of the radius (r). The distance between two consecutive layers can also be expressed in terms of the edge length (A) and the geometry of the arrangement:
H=2√2r√3=4r√3
Thus, the vertical distance between any two consecutive A layers in a cubic close-packed arrangement is:
H=4r√3
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The distance between two consecutive antinodes is
Aλ4Bλ2CλD2λ - Question 2 - Select One
The distance between two consecutive antinodes is,
A2λ,Bλ4Cλ2Dλ - Question 3 - Select One
Distance between two consecutive crests is
AλBλ/2Cλ4D2λ
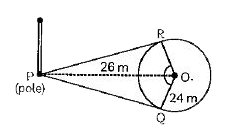
If six trees are to be planted along each tangential line segments at equal distances, find the distance between any two consecutive trees.View SolutionThe distance between two consecutive base pairs in DNA is
View SolutionHow much is the difference of time between any two consecutive longitudes?
View Solution6 equidistant vertical lines are drawn on a board. 6 equidistant horizontal lines are also drawn on the board cutting the 6 vertical lines, and the distance between any two consecutive horizontal lines is equal to that between any two consecutive vertical lines. What is the maximum number of squares thus formed?
View SolutionThe radius of gyration of a solid sphere of radius R about a certain axis is also equal to R. If r is the distance between the axis and the centre of the sphere, then r is equal to
View Solution

