Experimentally it was found that a metal oxide has formula M0.98O. Metal M is present as M2+andM3+ in iyts oxide. Fraction of the metal which exists as M3+ would be
0.0508
0.0701
0.0408
0.0605
The correct Answer is:b
To solve the problem, we need to determine the fraction of the metal M that exists as M3+ in the oxide M0.98O.
1. Identify the Formula and Oxidation States:
The given formula of the metal oxide is M0.98O. In this oxide, metal M can exist in two oxidation states: M2+ and M3+.
2. Determine the Total Charge from Oxygen:
Oxygen in the oxide has an oxidation state of −2. Since there is one oxygen atom, the total negative charge contributed by oxygen is −2.
3. Set Up the Charge Balance Equation:
Let x be the fraction of metal M that is in the M3+ state. Therefore, the fraction of metal M in the M2+ state will be 0.98−x. The total positive charge contributed by the metal can be expressed as:
3x+2(0.98−x)=2
Here, 3x is the contribution from M3+ and 2(0.98−x) is from M2+.
4. Simplify the Equation:
Expanding the equation gives:
3x+1.96−2x=2
Simplifying this results in:
x+1.96=2
5. Solve for x:
Subtract 1.96 from both sides:
x=2−1.96=0.04
6. Calculate the Fraction of M3+:
The fraction of metal M that exists as M3+ is x=0.04.
7. Calculate the Total Fraction of Metal:
To find the fraction of the total metal that is M3+, we divide by the total amount of metal:
Fraction of M3+=x0.98=0.040.98≈0.0408
Final Answer:
The fraction of the metal which exists as M3+ is approximately 0.0408 or 4.08%.
The given formula of the metal oxide is M0.98O. In this oxide, metal M can exist in two oxidation states: M2+ and M3+.
Oxygen in the oxide has an oxidation state of −2. Since there is one oxygen atom, the total negative charge contributed by oxygen is −2.
Let x be the fraction of metal M that is in the M3+ state. Therefore, the fraction of metal M in the M2+ state will be 0.98−x. The total positive charge contributed by the metal can be expressed as:
3x+2(0.98−x)=2
Here, 3x is the contribution from M3+ and 2(0.98−x) is from M2+.
Expanding the equation gives:
3x+1.96−2x=2
Simplifying this results in:
x+1.96=2
Subtract 1.96 from both sides:
x=2−1.96=0.04
The fraction of metal M that exists as M3+ is x=0.04.
To find the fraction of the total metal that is M3+, we divide by the total amount of metal:
Fraction of M3+=x0.98=0.040.98≈0.0408
The fraction of the metal which exists as M3+ is approximately 0.0408 or 4.08%.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Experimentally it was found that a metal oxide has formula M0.98O. Metal M is presented as M2+andM3+ in its oxide. Fraction of the metal which exists as M3+ would be
A5.08%B7.01%C4.08%D6.05% - Question 2 - Select One
Experimentally it was found that a metal oxide has formula M0.98O. Metal M present as M2+ and M3+ in its oxide. Fraction of the metal which exists as M3+ would be:
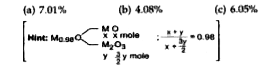 A0.0701B0.0408C0.0605D0.0508
A0.0701B0.0408C0.0605D0.0508 - Question 3 - Select One
Experimentally it was found that a metal oxide has formula M0.98O. Metal M present as M2+ and M3+ in its oxide. Fraction of the metal which exists as M3+ would be:
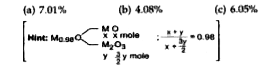 A5.08%B7.01%C4.08%D6.05%
A5.08%B7.01%C4.08%D6.05%
Analysis shows that a metal oxide has the empirical formula M0.96O1.00. Calculate the percentage of M2+ and M3+ ions in the sample.
View SolutionExperimentally it was found that a metal oxide in formula M0.98O. Metal M is present as M2+ and M3+ in its oxide ,Fraction of the metal which exists as M3+ would be
View SolutionExperimentally it was found that a metal oxide has formula M0.98, Metal M, is present as M+2 and M+3 in its oxid. Fraction of the metal which exist as M_(+3) would be :
View SolutionExperimentally it was found that a metal oxide has dormula M0.98O. Metal M, present as M2+andM3+ in its oxide. Fraction of the metal which exist as M3+andM3+ in its oxide. Fraction of the metal which exists as M3+ would be:
View SolutionExperimentally it is was found that a metal oxide has formula M0.95O .Metal M present as M3+ in its oxide fraction of the metal which exits as M2+ would be
View Solution

