Schrodinger wave equation for a particle in a one-dimension box is
δ2ψδx2+2mh(E−∞)ψ=0
δ2ψδx2+8π2mh2(E−V)ψ=0
δ2ψδx2+2mh(E−V)ψ=0
δ2ψδx2+2π2mh2(E−∞)=0
The correct Answer is:B
Schrodinger wave equation for a particel in one dimension box is
δ2Ψδx2+8π2mh2(E−V)Ψ=0
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - STRUCTURE OF ATOMEXERCISE - Competition Focus (JEE (Main and Advanced)/Medical Entrance (II. Multiple Choice Question)9videos
STRUCTURE OF ATOM
- BOOK - PRADEEPCHAPTER - STRUCTURE OF ATOMEXERCISE - Competition Focus (JEE (Main and Advanced)/Medical Entrance (III. Multiple Choice Question) (Based on Comprehension)20videos
STRUCTURE OF ATOM
- BOOK - PRADEEPCHAPTER - STRUCTURE OF ATOMEXERCISE - Analytical Questions And Problems with Answers/solutions (Problems)18videos
STRUCTURE OF ATOM
- BOOK - PRADEEPCHAPTER - STATES OF MATTER: SOLID MATTEREXERCISE - COMPETITION FOCUS (ASSERTION-REASON)17videos
STATES OF MATTER: SOLID MATTER
- BOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - MULTIPLE CHOICE QUESTION ( BASED ON PRACTICAL CHEMISTRY)3videos
THERMODYNAMICS
Similar Questions
Knowledge Check
- Question 1 - Select One
In the Schrodinger equation, H is
Aa mathematical operator called HamiltonianBconstructed by Schrodinger from the expression for the total energy of the systemCBoth (1) and (2)DNeither (1) nor (2) true - Question 2 - Select One
In the Schrodinger's wave equation Ψ represents
AorbitBwave functionCwaveDradial probability - Question 3 - Select One
In the Schrodingers wave equation sπ repressents
AOrbitBWave functionCWaveDRadial probability
On solving Schrodinger wave equation for hydrogen atom, the values of the enery obtained are called......and the corresponding values of the wavefunction (Ψ) are called.......
View SolutionDraw the v-t graphs for the given a-t graphs for a particle moving in one dimension.
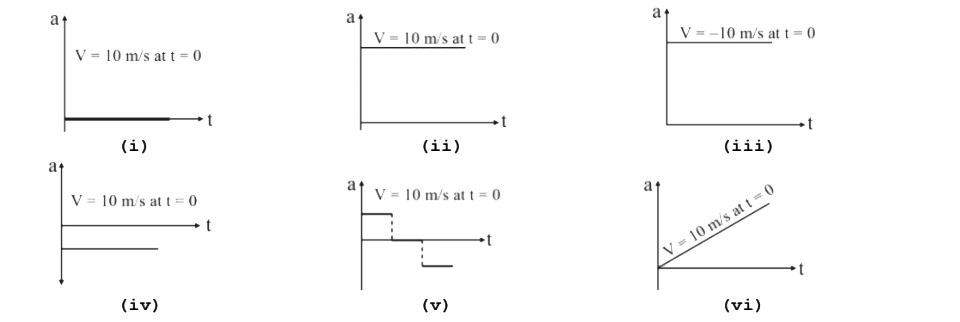 View Solution
View SolutionFind the particular solution of the time dependet Schrodinger equation for a freely moving particle of mass m.
View SolutionThe correct Schrodingers's wave equation for an electron with e as tatal energy and V as potential energy is :
View SolutionThe Schrodinger equation for a free electron of mass m and energy W written in terms of the wave function Ψ is d1Ψdx2+8π2mEh2Ψ=0. The dimensions of the coefficient of Ψ in the second term must be
View Solution

