Specific heat of an elementary gas is found to be 0.313 J at constant volume. If the molar mass of the gas is 40 g mol−1 , what is the atomicity of the gas ?
The correct Answer is:monoatomic
To determine the atomicity of the gas given its specific heat at constant volume (Cv) and molar mass, we can follow these steps:
Step 1: Identify the given values
- Specific heat at constant volume (Cv) = 0.313 J/g·K
- Molar mass of the gas (M) = 40 g/mol
Step 2: Calculate Cv in terms of J/mol·K
To convert the specific heat from J/g·K to J/mol·K, we use the formula:
Cv=Sv×M
Where:
- Sv = specific heat at constant volume (0.313 J/g·K)
- M = molar mass (40 g/mol)
Calculating:
Cv=0.313J/g⋅K×40g/mol=12.52J/mol⋅K
Step 3: Calculate Cp using the relation Cp = Cv + R
The relation between the specific heats at constant pressure and constant volume is given by:
Cp=Cv+R
Where:
- R = universal gas constant = 8.314 J/mol·K
Calculating:
Cp=12.52J/mol⋅K+8.314J/mol⋅K=20.834J/mol⋅K
Step 4: Calculate the ratio of Cp to Cv (γ)
The ratio of specific heats (γ) is given by:
γ=CpCv
Calculating:
γ=20.834J/mol⋅K12.52J/mol⋅K≈1.666
Step 5: Relate γ to atomicity (F)
For an ideal gas, the relationship between γ and the degrees of freedom (F) is given by:
γ=1+2F
Rearranging this equation to find F:
γ−1=2F
F=2γ−1
Substituting the value of γ:
F=21.666−1=20.666≈3
Step 6: Determine the atomicity of the gas
The degrees of freedom (F) for a monoatomic gas is 3, which indicates that the gas is monoatomic.
Final Answer
The atomicity of the gas is 1 (indicating it is a monoatomic gas).
---
- Specific heat at constant volume (Cv) = 0.313 J/g·K
- Molar mass of the gas (M) = 40 g/mol
To convert the specific heat from J/g·K to J/mol·K, we use the formula:
Cv=Sv×M
Where:
- Sv = specific heat at constant volume (0.313 J/g·K)
- M = molar mass (40 g/mol)
Cv=0.313J/g⋅K×40g/mol=12.52J/mol⋅K
The relation between the specific heats at constant pressure and constant volume is given by:
Cp=Cv+R
Where:
- R = universal gas constant = 8.314 J/mol·K
Cp=12.52J/mol⋅K+8.314J/mol⋅K=20.834J/mol⋅K
The ratio of specific heats (γ) is given by:
γ=CpCv
γ=20.834J/mol⋅K12.52J/mol⋅K≈1.666
For an ideal gas, the relationship between γ and the degrees of freedom (F) is given by:
γ=1+2F
γ−1=2F
F=2γ−1
F=21.666−1=20.666≈3
The degrees of freedom (F) for a monoatomic gas is 3, which indicates that the gas is monoatomic.
The atomicity of the gas is 1 (indicating it is a monoatomic gas).
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - PROBLEM FOR PRACTICE79videos
THERMODYNAMICS
- BOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - CURIOSITY QUESTIONS4videos
THERMODYNAMICS
- BOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - 333901videos
THERMODYNAMICS
- BOOK - PRADEEPCHAPTER - STRUCTURE OF ATOMEXERCISE - Competition Focus (JEE (Main and Advanced)/Medical Entrance (IX. Assertion And Reason Type Questions (Type II))12videos
STRUCTURE OF ATOM
Similar Questions
Molar heat capacity of a gas at constant volume.
View SolutionThe molar specific heats of an ideal gas at constant volume and constant pressure are respectively 4.98 and 6.96 cal mol−1K−1. If the molecular weight of the gas be 32, then calculate the root means square speed of the molecule of the gas at 120∘C. (1 cal = 4.2 J)
View Solution
Knowledge Check
- Question 1 - Select One
The specific heat of gas is found to be 0.075 calories at constant volume and its formula weight is 40. The atomicity of the gas would be
AOneBTwoCThreeDFour - Question 2 - Select One
Molar specific heat at constant volume Cv for a monatomic gas is
A32RB52RC3RD2R - Question 3 - Select One
Graph for specific heat at constant volume for a monoatomic gas
A B
B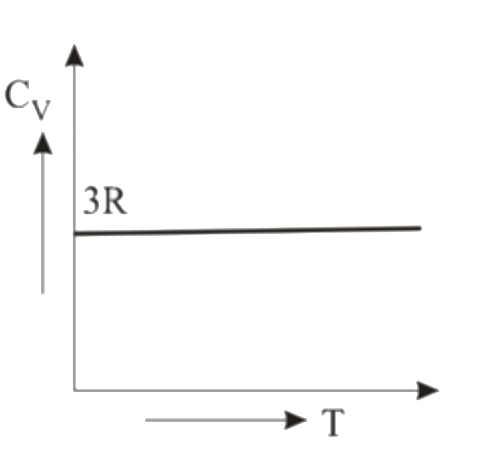 C
C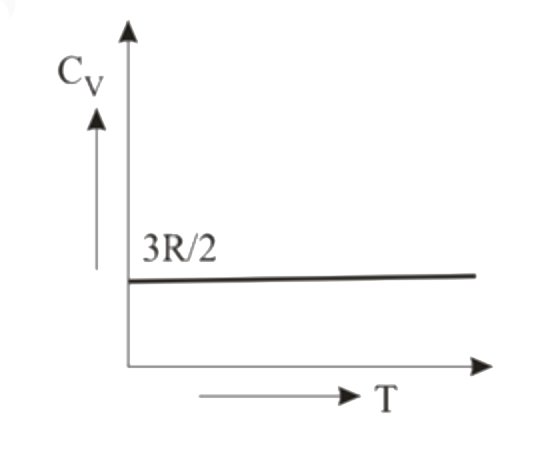 D
D
The specific heats of an ideal gas at constant volume and constant pressure are respectively 4.98 and 6.96 cal mol−1K−1. If the molecular weight of the gas be 32, then calculate the root-mean square speed of the molecules of the gas at 120∘C, (1 cal=4.2J)
View SolutionThe specific heat of a monoatomic gas at constant pressure is 248.2 J kg−1K−1 and at constant volume it is 149.0 J kg−1K−1. Find the mean molar mass of the gas.
View SolutionIf the molar specific heat of a gas at constant pressure is 72R, then the atomicity of gas is
View SolutionGraph for specific heat at constant volume for a monoatomic gas
View SolutionThe molar specific heat at constant volume, for a non linear triatomic gas is
View Solution

