Which one of the following is correct when an ideal gas is expanded adaibatically and reversibly ?
q=0,W=nCvdT,ΔU=nCvdT
q=0,W=0,ΔU=nCvdT
q=0,W=nCvd,ΔU=0
None of the above
The correct Answer is:A
To solve the question regarding the behavior of an ideal gas during an adiabatic and reversible expansion, we can follow these steps:
1. Understand the Adiabatic Process:
- In an adiabatic process, there is no heat exchange with the surroundings. Therefore, the heat energy Q=0.
2. Apply the First Law of Thermodynamics:
- The first law of thermodynamics states:
ΔU=Q+W
- Since Q=0 for an adiabatic process, the equation simplifies to:
ΔU=W
3. Relate Change in Internal Energy to Work Done:
- The change in internal energy ΔU for an ideal gas can be expressed as:
ΔU=nCVΔT
- Here, n is the number of moles, CV is the molar heat capacity at constant volume, and ΔT is the change in temperature.
4. Express Work Done in Terms of Internal Energy:
- From the first law, we established that W=ΔU. Therefore, we can write:
W=nCVΔT
5. Summarize the Relationships:
- For an ideal gas expanded adiabatically and reversibly:
- Heat exchanged Q=0
- Work done W=nCVΔT
- Change in internal energy ΔU=nCVΔT
6. Identify the Correct Statement:
- The correct statement regarding the adiabatic expansion of an ideal gas is:
- Q=0, W=nCVΔT, and ΔU=nCVΔT.
Conclusion:
Thus, the correct option is that during an adiabatic and reversible expansion of an ideal gas, the heat exchange is zero, and the work done equals the change in internal energy.
- In an adiabatic process, there is no heat exchange with the surroundings. Therefore, the heat energy Q=0.
- The first law of thermodynamics states:
ΔU=Q+W
- Since Q=0 for an adiabatic process, the equation simplifies to:
ΔU=W
- The change in internal energy ΔU for an ideal gas can be expressed as:
ΔU=nCVΔT
- Here, n is the number of moles, CV is the molar heat capacity at constant volume, and ΔT is the change in temperature.
- From the first law, we established that W=ΔU. Therefore, we can write:
W=nCVΔT
- For an ideal gas expanded adiabatically and reversibly:
- Heat exchanged Q=0
- Work done W=nCVΔT
- Change in internal energy ΔU=nCVΔT
- The correct statement regarding the adiabatic expansion of an ideal gas is:
- Q=0, W=nCVΔT, and ΔU=nCVΔT.
Thus, the correct option is that during an adiabatic and reversible expansion of an ideal gas, the heat exchange is zero, and the work done equals the change in internal energy.
Topper's Solved these Questions
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Comprehension 1
1 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Comprehension 2
2 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - SHORT ANSWER QUESTIONS
65 Videos
- STRUCTURE OF ATOMBOOK - PRADEEPCHAPTER - STRUCTURE OF ATOMEXERCISE - Competition Focus (JEE (Main and Advanced)/Medical Entrance (IX. Assertion And Reason Type Questions (Type II))
12 Videos
Similar Questions
Knowledge Check
Which of the following curve is correct for an ideal gas ?
A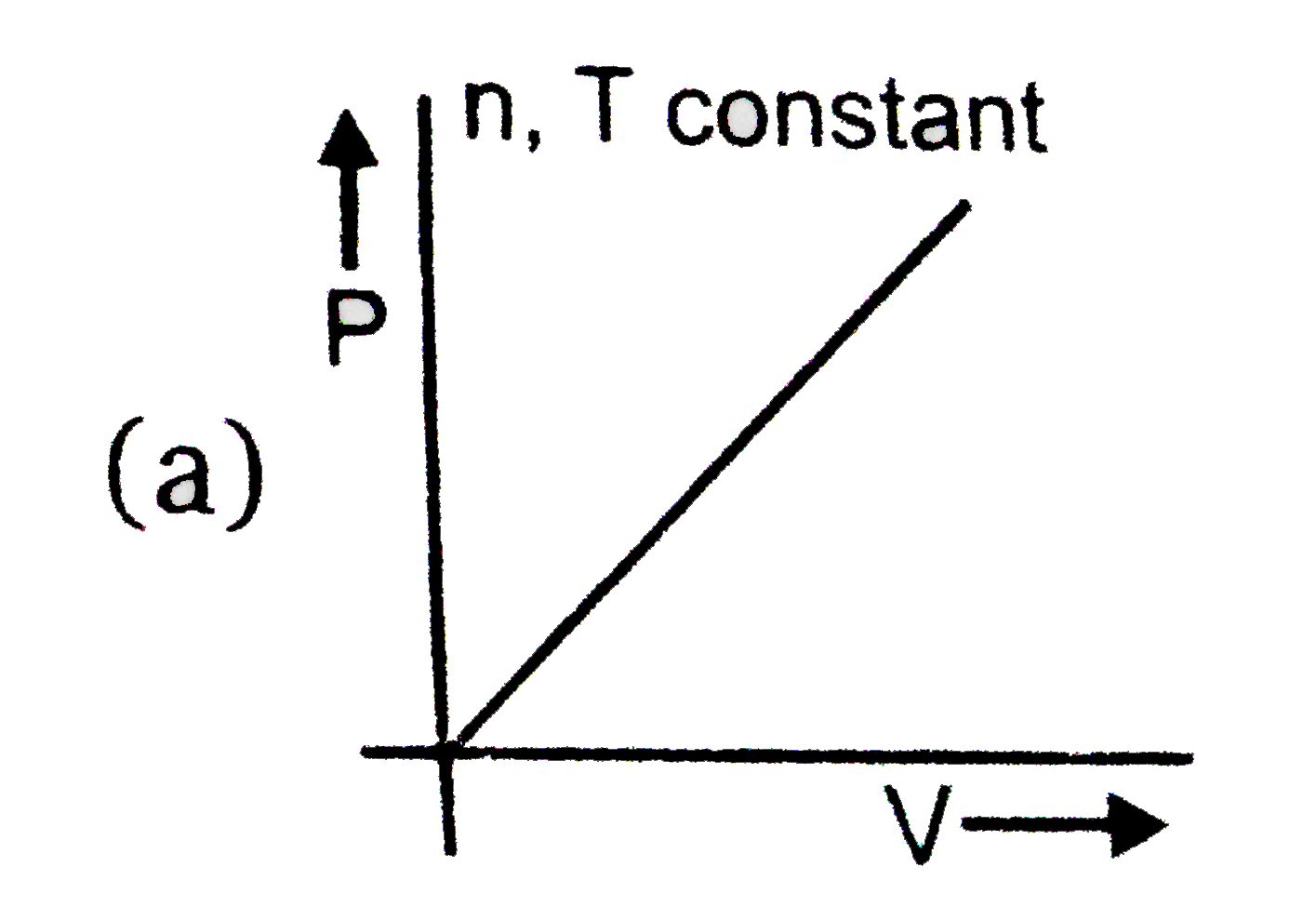 B
B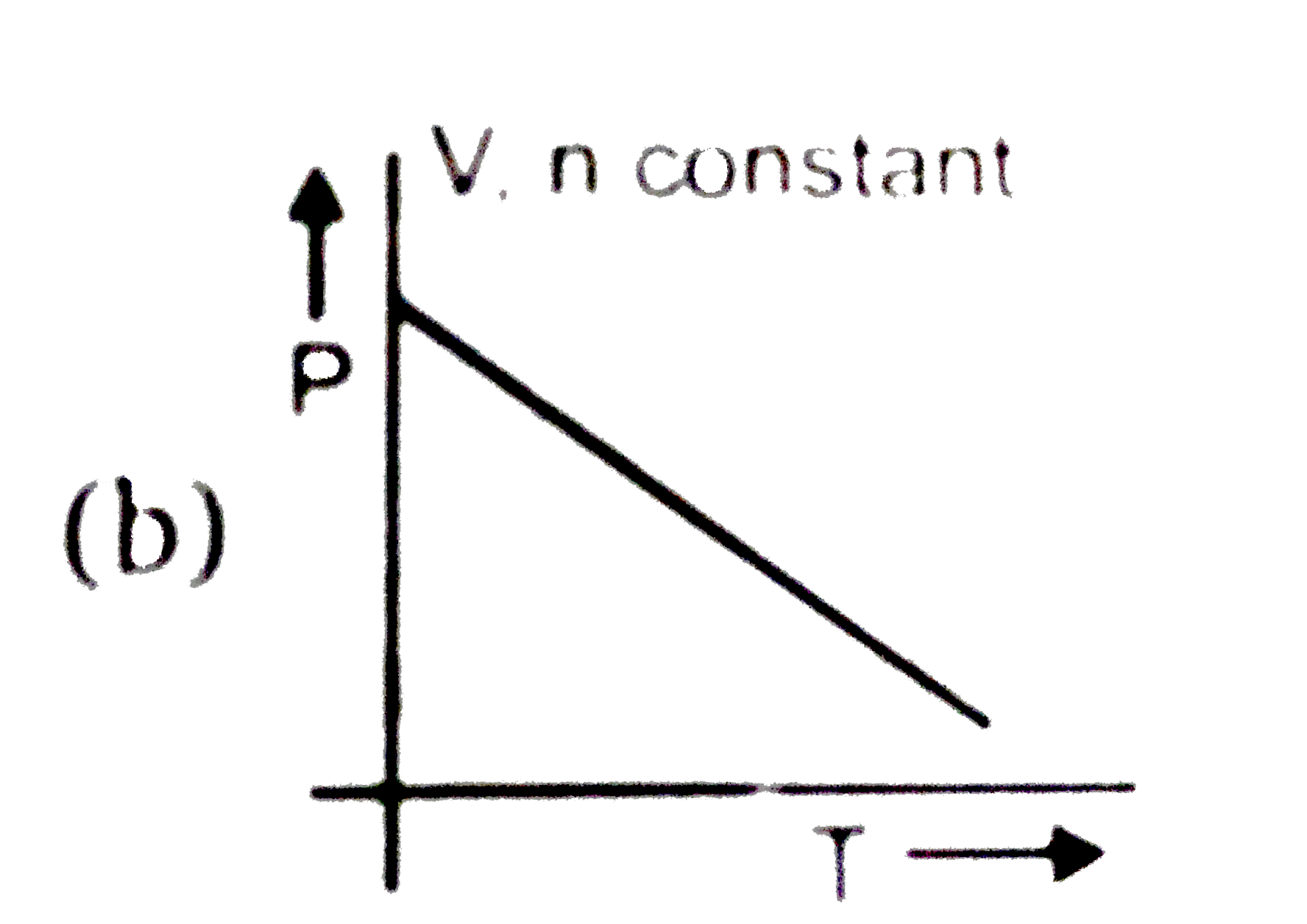 C
C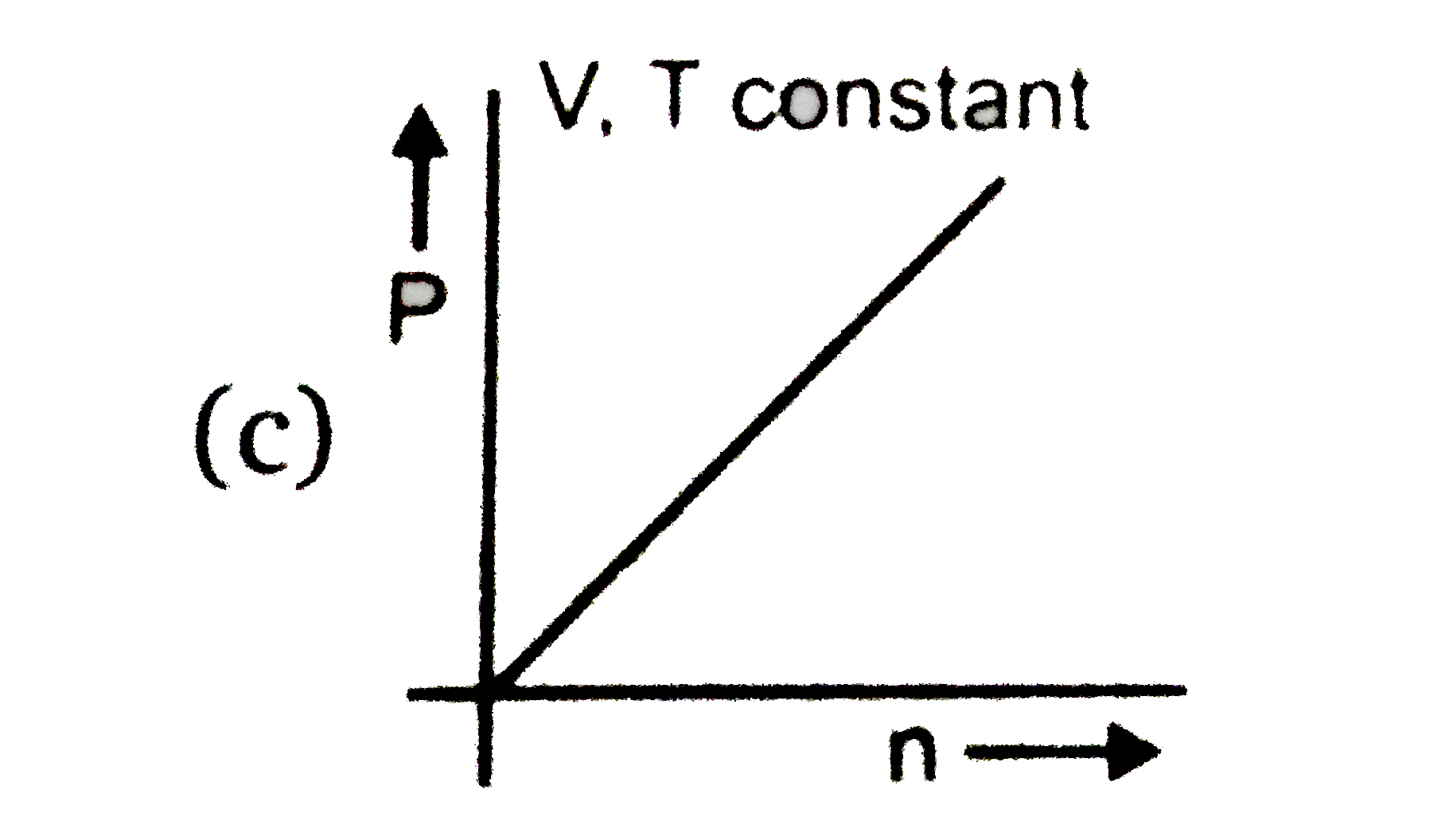 D
D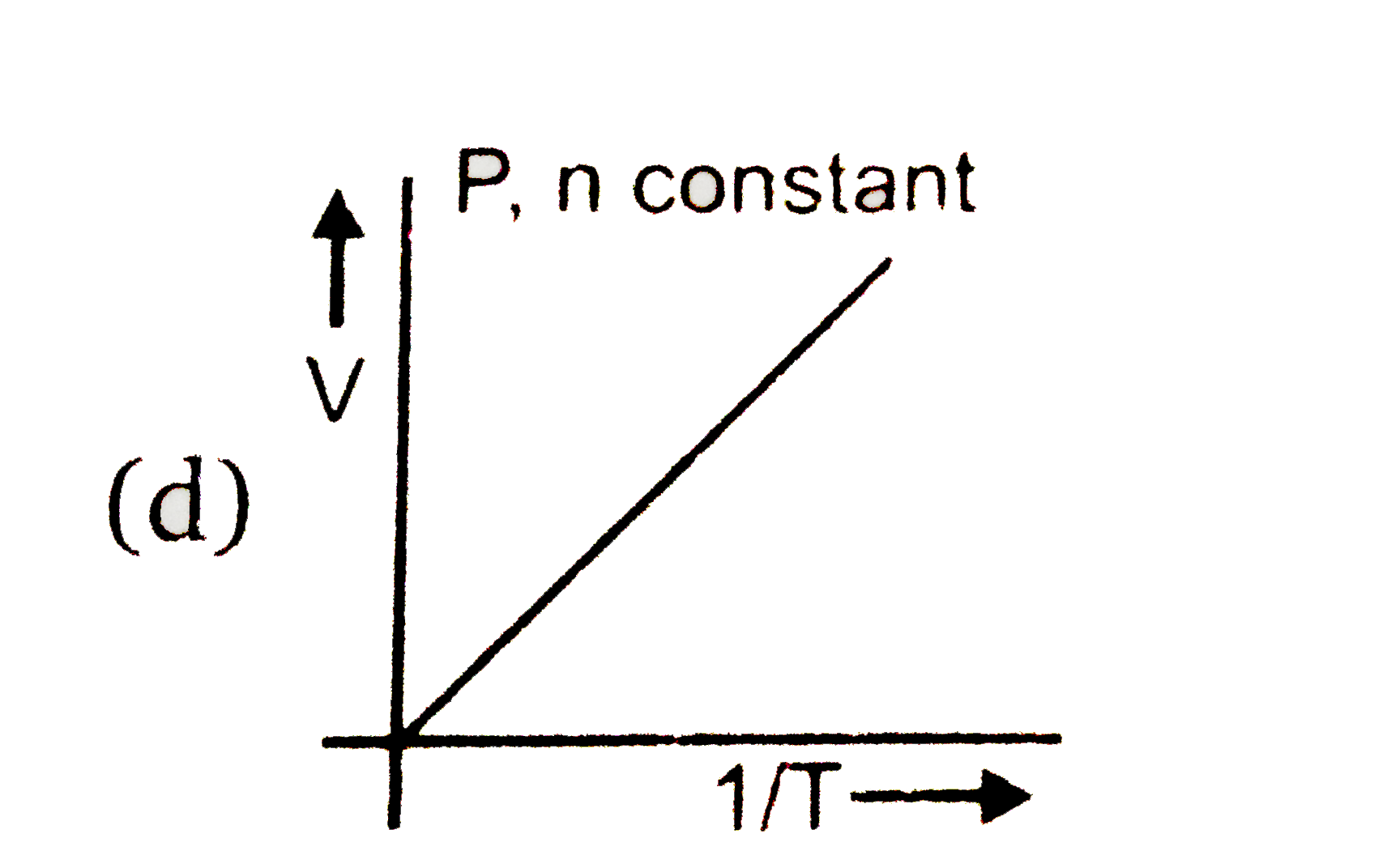
Which of the following plots are correct for an ideal gas ?
A B
B C
C D
D
Which of the following expressions is correct for an ideal gas?
AP=23VNA¯¯¯EBP=32vNA¯¯¯ECP=23NAV¯¯¯EDP=32NAV¯¯¯E
Which of the following expressions are correct for an ideal gas ?
View SolutionFor an ideal gas expanding adiabatically in vacuum,
View SolutionWhich of the following is correct for adiabatic expansion ideal gas?
View SolutionWhich of the following statements is CORRECT for an ideal gas ?
View SolutionWhich is (are) correct for ideal gas ?
View Solution
