A : After menopause the levels of blood gonadotropins will rise markedly .
R : At the time of menopause all the ovarian follicles are converted into follicular atresia and the ovaries are not responding to the gonadotropins
If both Assertion & Reason are true and the reason is the correct explanation of the assertion then mark (1)
If both Assertion & Reason are true but the reason is not the correct explanation of the assertion then mark (2)
If Assertion is true statement but Reason is false then mark (3)
If both Assertion and Reason are false statement then Mark (4)
The correct Answer is:B
Step by step video, text & image solution for A : After menopause the levels of blood gonadotropins will rise markedly . R : At the time of menopause all the ovarian follicles are converted into follicular atresia and the ovaries are not responding to the gonadotropins by Biology experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- HUMAN REPRODUCTIONBOOK - AAKASH INSTITUTECHAPTER - HUMAN REPRODUCTIONEXERCISE - Try Yourself
17 Videos
- HUMAN REPRODUCTIONBOOK - AAKASH INSTITUTECHAPTER - HUMAN REPRODUCTIONEXERCISE - Assignment ( Section - C ) (Previous Type Question )
81 Videos
- EXCRETORY PRODUCTS AND THEIR ELIMINATIONBOOK - AAKASH INSTITUTECHAPTER - EXCRETORY PRODUCTS AND THEIR ELIMINATIONEXERCISE - SECTION D ( ASSERTIN-REASON TYPE QUASTION)
10 Videos
- LOCOMOTION AND MOVEMENTBOOK - AAKASH INSTITUTECHAPTER - LOCOMOTION AND MOVEMENTEXERCISE - ASSIGNMENT SECTION-D
10 Videos
Similar Questions
(a) Explain the menstrual phase in a human female. State the levels of ovarian and pituitary hormones during this phase.
(b) Why is follicular phase in the menstrual cycle also referred as proliferative phase ? Explain.
(c) Explain the events that occur in a graafian follicle at the time of ovulation and thereafter. ltbvrgt (d) Draw a graafian follicle and label antrum and secondary oocyte.
View SolutionDirection: Below a passage is given after which you will find some items based on the passage. First, read the passage and answer the items based on it. You are required to select your answers based on the contents of the passage and opinion of the author only.
Over-eating is one of the most wonderful practices among those who think that they can afford it. In fact, authorities say that nearly all who can get as much as they desire, over-eat to their disadvantage. This class of people could save a great more food than they can save by missing one meal per week and at the same time they could improve their health. A heavy meal at night, the so-called "dinner", is the fashion with many and often is taken shortly before retiring. It is unnecessary and could be forgone, not only once a week but daily without loss of strength. From three to five hours are needed to digest food. While sleeping, this food not being required to give energy for work, is in many cases converted into excess fat, giving rise to over-weight. The evening meal should be light, taken three or four hours before retiring. This prevents over-eating, conserves energy and reduces the cost of food.
According to the passage, how many times a day should we have food ?
View Solution
Knowledge Check
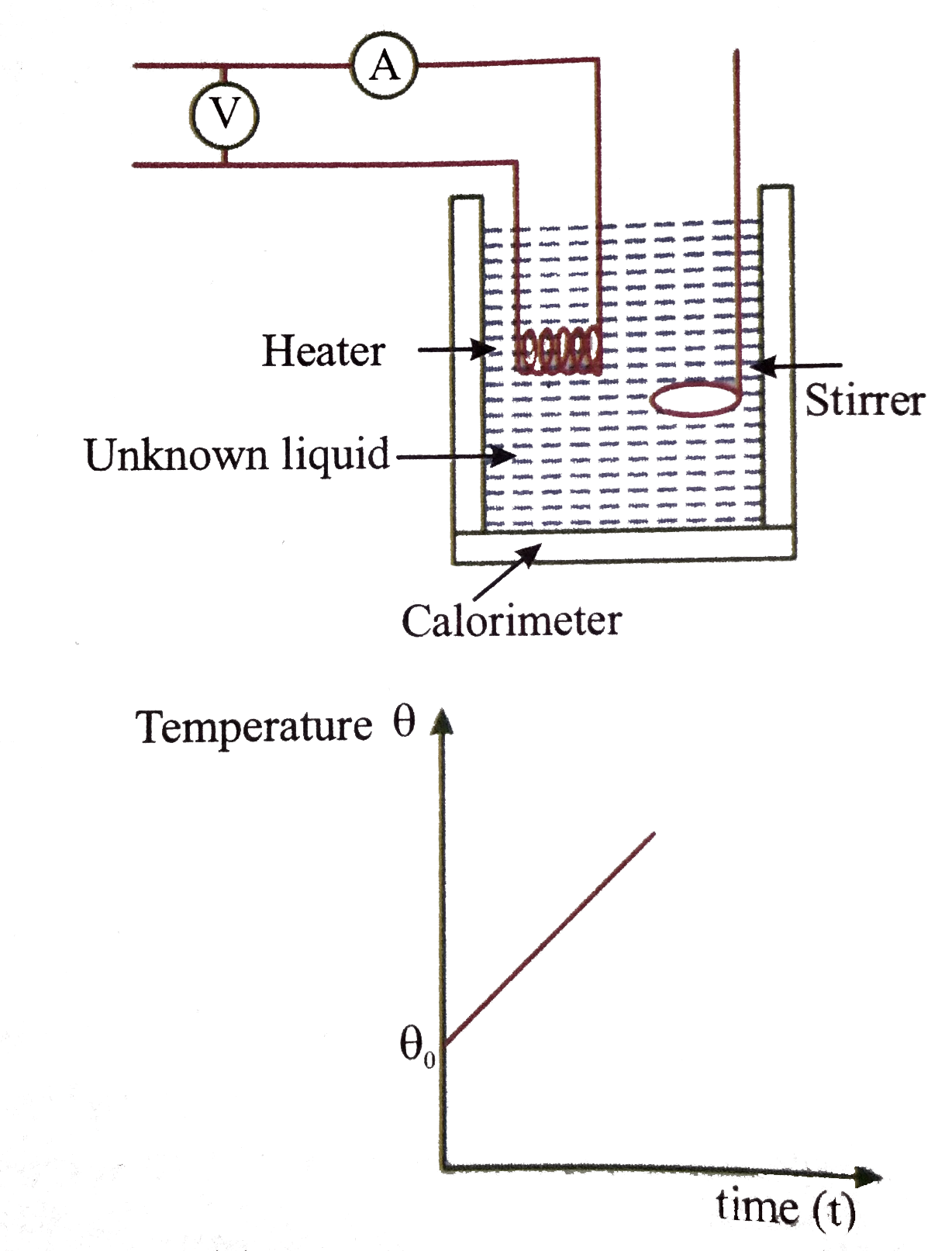
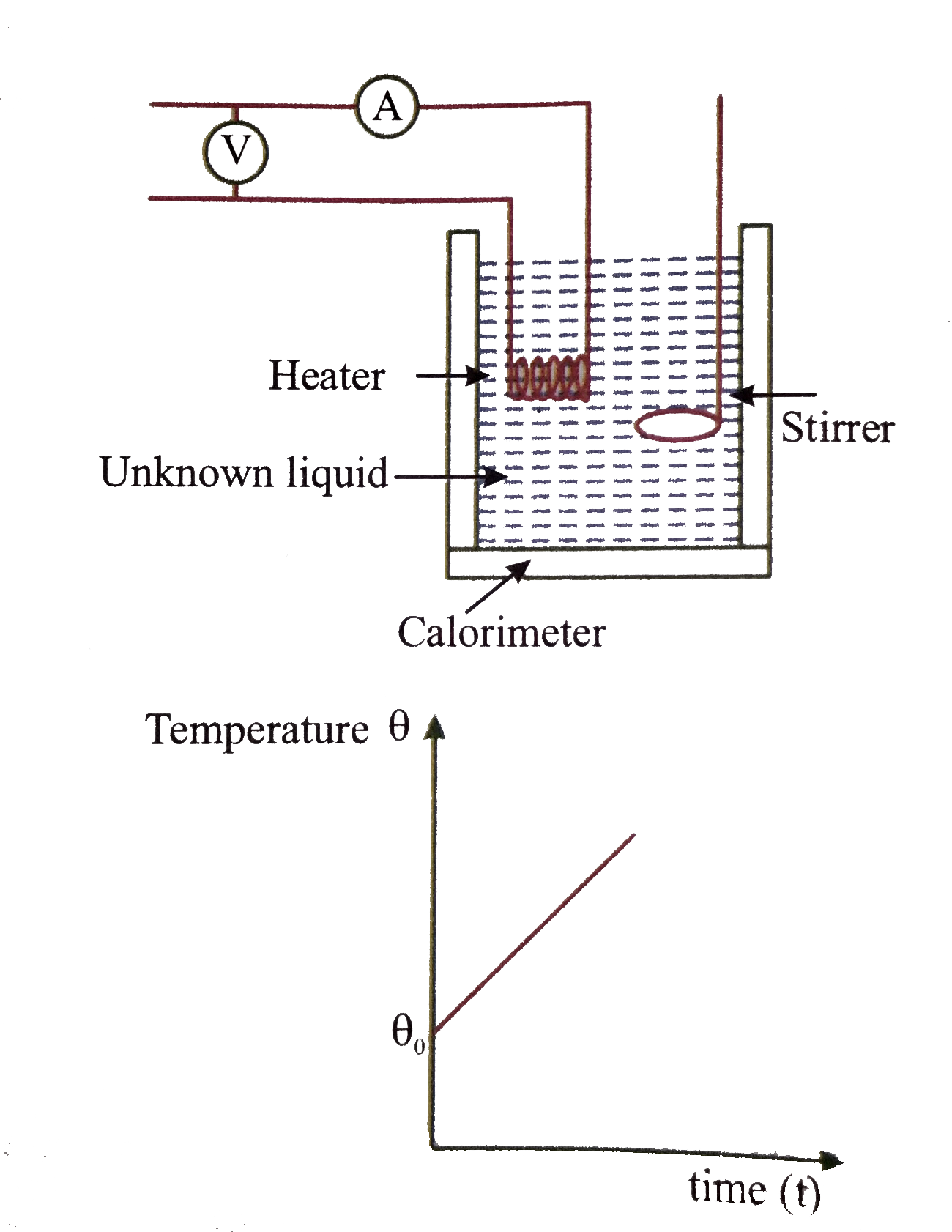
Figure shows an electrical calorimeter to determine specific heat capacity of an unknown liquid, First of all, the mass of empty calorimeter (a copper container) is measured and suppose it is m1. Then the unknown liquid is poured in it. Now the combined mass of calorimeter+liquid system is measured and let it be m2. So the mass of liquid is (m2−m1). Initially both were at room temperature (θ0).
Now a heater is immeresed in if for time interval t. The voltage drop across the heater is V and current passing through it is I. Due to heat supplied, the temperature of both the liquid and calorimeter will rise simultaneously. After tsec, heater was switched off, and final temperature is θr. If there is no heat loss to surroundings. Heat supplied by the heater=Heat absorbed by the liquid+heat absorbed by the calorimeter (VI)t=(m2−m1)S1(θf−θ0)+m1Sc(θf−θ0)
The specific heat of the liquid S1=(VI)tθf−θ0−m1Sc(m2−m1)
Radiation correction: There can be heat loss to environment. To compensate this loss, a correction is introduced.
Let the heater was on for tsec, and then it is switched off. Now the temperature of the mixture falls due to heat loss to environment. The temperature of the mixture is measured t/2sec. after switching off. Let the fall in temperature during this time is ɛ
Now the corrected final temperature is taken as θf=θf+ɛ
In this experiment voltage across the heater is 100.0V and current is 10.0A, and heater was switched on for t=700.0sec. Initially all elements were at room temperature θ∘=10.0∘C and final temperature was measured as θf=73.0∘C.
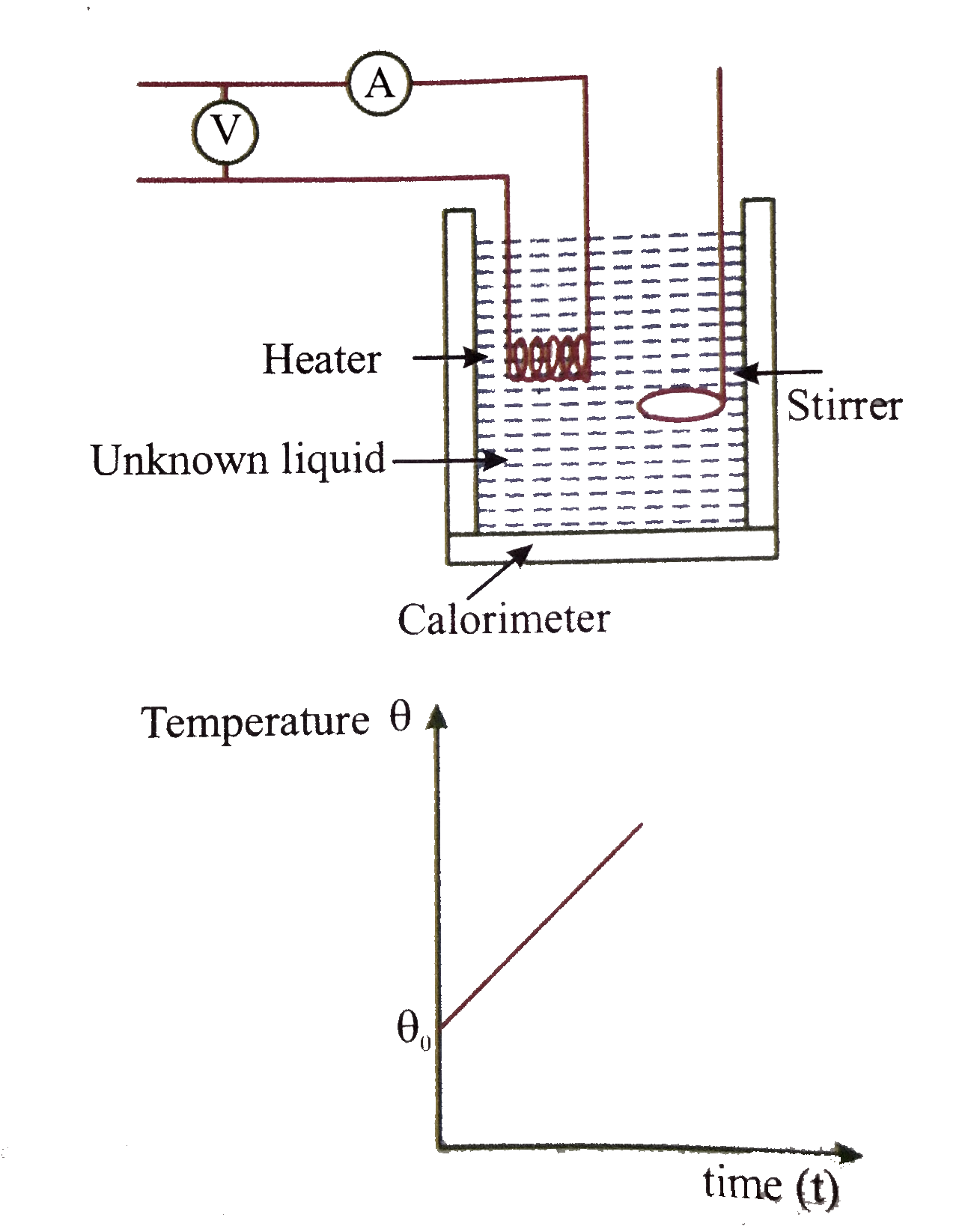
Mass of empty calorimeter ws 1.0kg and the combined mass of calorimeter + liquid is 3.0kg. The specific heat capacity of the calorimeter =3.0×103J/kg∘C. The falls in temperature 350 second after switching off the heater was 7.0∘C. Find the specific heat capacity of the unknown liquid in proper significant figures.A3.5×103J/kg∘CB3.50×103J/kg∘CC4.0×103J/kg∘CD3.500×103J/kg∘CFigure shows an electrical calorimeter to determine specific heat capacity of an unknown liquid, First of all, the mass of empty calorimeter (a copper container) is measured and suppose it is m1. Then the unknown liquid is poured in it. Now the combined mass of calorimeter+liquid system is measured and let it be m2. So the mass of liquid is (m2−m1). Initially both were at room temperature (θ0).
Now a heater is immeresed in if for time interval t. The voltage drop across the heater is V and current passing through it is I. Due to heat supplied, the temperature of both the liquid and calorimeter will rise simultaneously. After tsec, heater was switched off, and final temperature is θr. If there is no heat loss to surroundings. Heat supplied by the heater=Heat absorbed by the liquid+heat absorbed by the calorimeter (VI)t=(m2−m1)S1(θf−θ0)+m1Sc(θf−θ0)
The specific heat of the liquid S1=(VI)tθf−θ0−m1Sc(m2−m1)
Radiation correction: There can be heat loss to environment. To compensate this loss, a correction is introduced.
Let the heater was on for tsec, and then it is switched off. Now the temperature of the mixture falls due to heat loss to environment. The temperature of the mixture is measured t/2sec. after switching off. Let the fall in temperature during this time is ɛ
Now the corrected final temperature is taken as θf=θf+ɛ
If the system were losing heat according to Newton's cooling law, the temperature of the mixture would change with time according to (while heater was on)A B
B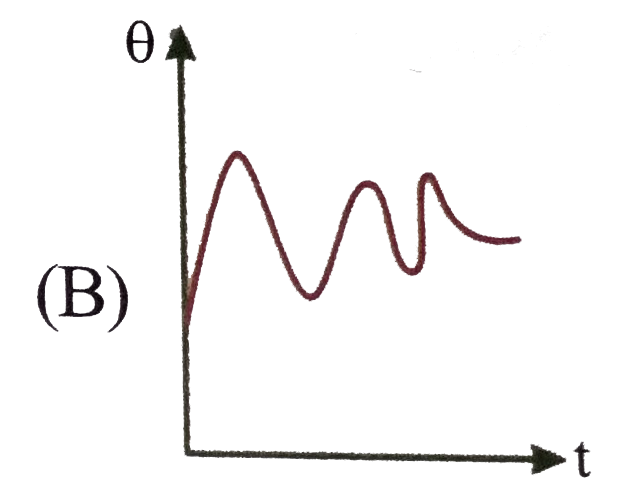 C
C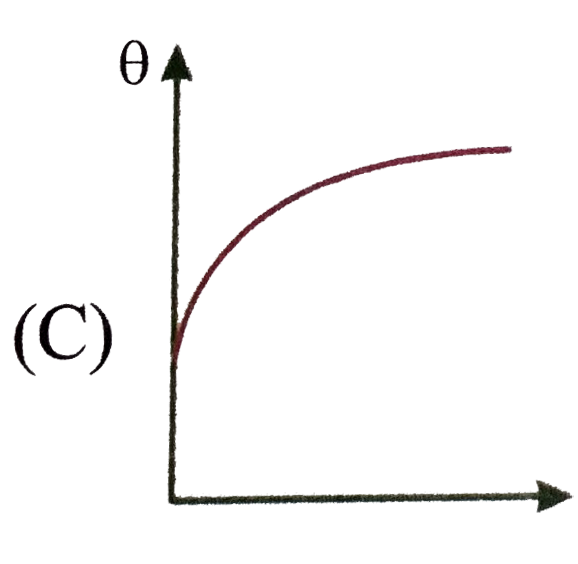 D
D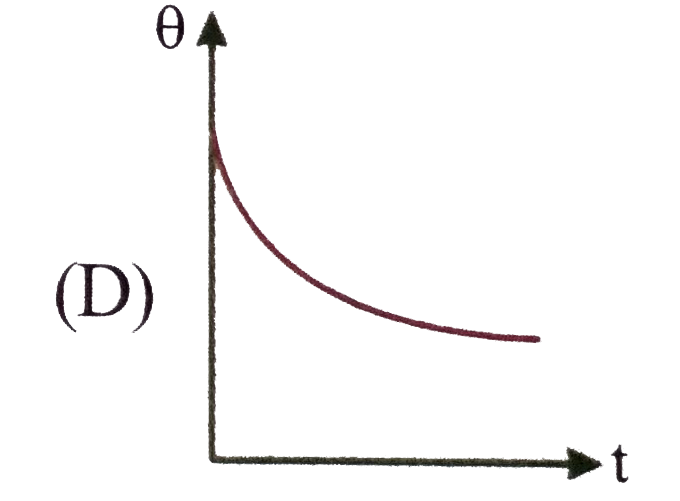
Figure shows an electrical calorimeter to determine specific heat capacity of an unknown liquid, First of all, the mass of empty calorimeter (a copper container) is measured and suppose it is m1. Then the unknown liquid is poured in it. Now the combined mass of calorimeter+liquid system is measured and let it be m2. So the mass of liquid is (m2−m1). Initially both were at room temperature (θ0).
Now a heater is immeresed in if for time interval t. The voltage drop across the heater is V and current passing through it is I. Due to heat supplied, the temperature of both the liquid and calorimeter will rise simultaneously. After tsec, heater was switched off, and final temperature is θr. If there is no heat loss to surroundings. Heat supplied by the heater=Heat absorbed by the liquid+heat absorbed by the calorimeter (VI)t=(m2−m1)S1(θf−θ0)+m1Sc(θf−θ0)
The specific heat of the liquid S1=(VI)tθf−θ0−m1Sc(m2−m1)
Radiation correction: There can be heat loss to environment. To compensate this loss, a correction is introduced.
Let the heater was on for tsec, and then it is switched off. Now the temperature of the mixture falls due to heat loss to environment. The temperature of the mixture is measured t/2sec. after switching off. Let the fall in temperature during this time is ɛ
Now the corrected final temperature is taken as θf=θf+ɛ
If mass and specific heat capacity of calorimeter is negligible, what would be maximum permissible error in Sl. Use the date mentioned below.
m1→, Sl→0, m2=1.00kg,
V=10.0V, I=10.0A,
t=1.00×102sec, θ0=15∘C,
Corrected θ1=65∘CA4%B5%C8%D12%
Direction: Below a passage is given after which you will find some items based on the passage. First, read the passage and answer the items based on it. You are required to select your answers based on the contents of the passage and opinion of the author only.
Over-eating is one of the most wonderful practices among those who think that they can afford it. In fact, authorities say that nearly all who can get as much as they desire, over-eat to their disadvantage. This class of people could save a great more food than they can save by missing one meal per week and at the same time they could improve their health. A heavy meal at night, the so-called "dinner", is the fashion with many and often is taken shortly before retiring. It is unnecessary and could be forgone, not only once a week but daily without loss of strength. From three to five hours are needed to digest food. While sleeping, this food not being required to give energy for work, is in many cases converted into excess fat, giving rise to over-weight. The evening meal should be light, taken three or four hours before retiring. This prevents over-eating, conserves energy and reduces the cost of food.
Why should those who over-eat refrain from doing so ?
View SolutionDirection: Below a passage is given after which you will find some items based on the passage. First, read the passage and answer the items based on it. You are required to select your answers based on the contents of the passage and opinion of the author only.
Over-eating is one of the most wonderful practices among those who think that they can afford it. In fact, authorities say that nearly all who can get as much as they desire, over-eat to their disadvantage. This class of people could save a great more food than they can save by missing one meal per week and at the same time they could improve their health. A heavy meal at night, the so-called "dinner", is the fashion with many and often is taken shortly before retiring. It is unnecessary and could be forgone, not only once a week but daily without loss of strength. From three to five hours are needed to digest food. While sleeping, this food not being required to give energy for work, is in many cases converted into excess fat, giving rise to over-weight. The evening meal should be light, taken three or four hours before retiring. This prevents over-eating, conserves energy and reduces the cost of food.
According to the passage, people over eat
View SolutionWhy the chances of pregnancy are very low in a lactating women till six months after delievery?
a.)High levels of HCG in women kill sperms
b.)High levels of estrogen and progesterone, secreted by the corpus luteum, that inhibit the secretion of gonadotropins.
c.)High levels of prolactin, inhibit the secretion of gonadotropins
d.)All of these
View SolutionChoose the incorrect statement with reference to menstrual cycle
(A) Gonadotropins attain a peak level in the middle of the cycle
(B) Progesterone is secreted only during luteal phase
(C) "LH" surge induces rupture of the Graafian follicle resulting in ovulation
(D) Estrogen is secreted only during follicular phase
View SolutionRead the following news report news report and,
• Identify the governments at different levels.
• What elements of the working of judiciary and executive can you identify in it
• Identify the policy issues, matters related to legislation, implementation and interpretation of the law involved in this case.
Centre, Delhi join hands on CNG issue
By Our Staff Reporter, the Hindu 23 September 2001
NEW DELHI, SEPT. 22. The Centre and the Delhi Government today agreed to jointly approach the Supreme Court this coming week for phasing out of all non CNG commercial vehicles in the Capital. They also decided to seek a dual fuel policy for the city instead of putting the entire transportation system on the single - fuel mode ''which was full of dangers and would result in disaster.''
It was also decided to discourage the use of CNG by private vehicle owners in the Capital. Both governments would press for allowing the use of 0.05 per cent low sulphur diesel for running of buses in the Capital. In addition, it would be pleaded before the Court that all commercial vehicles, which fulfil the Euro - II standards, should be allowed to ply in the city. Though both the Centre and the State would file separate affidavits, these would contain common points. The Centre would also go out support the Delhi Government's stand on the issues concerniong CNG. These decisions were taken at a meeting between the Delhi Chief Minister, Ms. Sheila Dikshit, and the Union Petroleum and Natural Gas Minister, Mr. Ram Naik.
Ms. Dikshit said the Central Goverenment would request the court that in view of the high powered Committee appointed under Dr. R.A. Mashelkar to suggest an ''Auto Fuel Policy'' for the entire country, it would be appropriate to extand the deadline as it was not possible to convert the entire 10,000-odd bus fleet into CNG during the prescribed time frame. The Mashelkar Commitee is expected to submit its repoet within a period of six months.
The Chief Minister said time was required to implement the court directives. Referring to the coordinated approach on the issue, Ms. Dikshit said this would take into accont the details about the number of vehicles to be run on CNG, eliminating long queues outside CNG filling stations, the CNG fuel requirements of Delhi and the ways and means to implement the directive of the court.
The Supreme Court had . . . refused to relax the only CNG norm for the city's buses but said it had never insisted on CNG for taxis and auto rickshaws. Mr. Naik said the Centre would insist on allowing use of low sulphur diesel for buses in Delhi as putting the entire transportation system dependent on CNG could prove to be disastrous. The Capital relied on pipeline supply for CNG and any disruption would throw thw public transport system out of gear.
View Solution
