How many geometrical isomers are possible for [Zn(NH3)ClBrPPh3]− ?
Video Solution
Text Solution
The correct Answer is:0
|
Answer
Step by step video & image solution for How many geometrical isomers are possible for [Zn(NH_(3))ClBrPPh_(3)]^(-) ? by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- COORDINATION COMPOUNDS BOOK - AAKASH INSTITUTECHAPTER - COORDINATION COMPOUNDS EXERCISE - Assignment (Section-H Multiple True-False Type Questions )
5 Videos
- COORDINATION COMPOUNDS BOOK - AAKASH INSTITUTECHAPTER - COORDINATION COMPOUNDS EXERCISE - Assignment (Section-I Subjective Type Questions )
10 Videos
- COORDINATION COMPOUNDS BOOK - AAKASH INSTITUTECHAPTER - COORDINATION COMPOUNDS EXERCISE - Assignment (Section-F Matrix Match Type Questions )
3 Videos
- CLASSIFICATION OF ELEMENTS AND PERIODICITY IN PROPERTIESBOOK - AAKASH INSTITUTECHAPTER - CLASSIFICATION OF ELEMENTS AND PERIODICITY IN PROPERTIESEXERCISE - Assignment (Section - J Aakash Challengers Questions)
6 Videos
- ELECTROCHEMISTRY BOOK - AAKASH INSTITUTECHAPTER - ELECTROCHEMISTRY EXERCISE - Assignment (SECTION - J) (Aakash Challengers Questions)
10 Videos
Similar Questions
Knowledge Check
The number of geometrical isomers for octahedral [Co(NH3)2Cl4]− and square planar [AuCl2Br2]− respectively are :
ATwo cis and trans, no geometrical isomersBTwo cis and trans, two cis and transCNo geometrical isomers, two cis and transDNo geometrical isomers, no geometrical isomerHow many geometrical isomers are possible for [Pd2+(NH2−CH(CH3)−CO−2)2]∘ ?
A2B3C4D6How many geometrical isomers are possible for [Pd2+(NH2−CH(CH3)−CO−2)2]0
A2B3C4D6
How many type of geometrical isomers are possible for [M(NH3)BrCl(H2O)], where M is Pt+2 ?
View Solution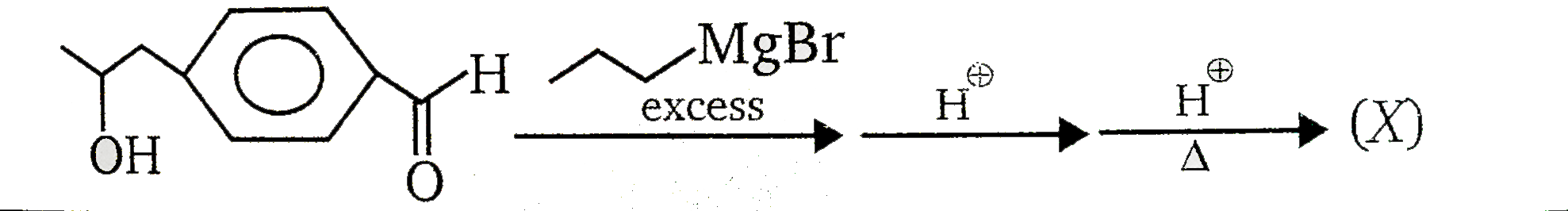
How many geometrical isomer of (X) is possible ?
View SolutionHow many geometrical isomers arepossible for [Pt(NO2)(NH2OH)(Py)]+?
View SolutionHow many geometrical isomers are possible for complex [Mab(AB)2]n±?
View SolutionHow many geometrical isomers are possible for complex [Mab(AB)2]n±?
View Solution