A particle is moving along x-axis such that its velocity varies with time according to v=(3m/s2)t−(2m/s3)t2. Find the velocity at t = 1 s and average velocity of the particle for the interval t = 0 to t = 5 s.
To solve the problem, we need to find the velocity of the particle at t=1 s and the average velocity over the interval from t=0 s to t=5 s.
Step 1: Find the velocity at t=1 s
The velocity of the particle is given by the equation:
v(t)=3t−2t2
To find the velocity at t=1 s, we substitute t=1 into the equation:
v(1)=3(1)−2(12)=3−2=1 m/s
Step 2: Find the average velocity from t=0 s to t=5 s
The average velocity ¯v over a time interval can be calculated using the formula:
¯v=x(5)−x(0)t(5)−t(0)
where x(t) is the displacement at time t.
To find x(5) and x(0), we need to integrate the velocity function v(t):
dx=v(t)dt=(3t−2t2)dt
Integrating from t=0 to t=5:
x(t)=∫(3t−2t2)dt
Calculating the integral:
x(t)=(3t22−2t33)+C
We can set C=0 since we are interested in displacement from the starting point.
Now, we evaluate x(5):
x(5)=3(52)2−2(53)3
Calculating each term:
x(5)=3(25)2−2(125)3=752−2503
To combine these fractions, we need a common denominator, which is 6:
x(5)=75⋅36−250⋅26=2256−5006=−2756
Now, we evaluate x(0):
x(0)=0 (since the particle starts at the origin)
Step 3: Calculate the average velocity
Now we can find the average velocity:
¯v=x(5)−x(0)5−0=(−2756−0)5=−2756⋅5=−27530=−556 m/s
Final Answers
1. The velocity at t=1 s is 1 m/s.
2. The average velocity from t=0 s to t=5 s is −556 m/s.
The velocity of the particle is given by the equation:
v(t)=3t−2t2
To find the velocity at t=1 s, we substitute t=1 into the equation:
v(1)=3(1)−2(12)=3−2=1 m/s
The average velocity ¯v over a time interval can be calculated using the formula:
¯v=x(5)−x(0)t(5)−t(0)
where x(t) is the displacement at time t.
dx=v(t)dt=(3t−2t2)dt
Integrating from t=0 to t=5:
x(t)=∫(3t−2t2)dt
Calculating the integral:
x(t)=(3t22−2t33)+C
We can set C=0 since we are interested in displacement from the starting point.
x(5)=3(52)2−2(53)3
Calculating each term:
x(5)=3(25)2−2(125)3=752−2503
To combine these fractions, we need a common denominator, which is 6:
x(5)=75⋅36−250⋅26=2256−5006=−2756
x(0)=0 (since the particle starts at the origin)
Now we can find the average velocity:
¯v=x(5)−x(0)5−0=(−2756−0)5=−2756⋅5=−27530=−556 m/s
1. The velocity at t=1 s is 1 m/s.
2. The average velocity from t=0 s to t=5 s is −556 m/s.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Try Yourself40videos
MOTION IN STRAIGHT LINE
- BOOK - AAKASH INSTITUTECHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - A)50videos
MOTION IN STRAIGHT LINE
- BOOK - AAKASH INSTITUTECHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - D)15videos
MOTION IN A STRAIGHT LINE
- BOOK - AAKASH INSTITUTECHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION D16videos
MOVING CHARGE AND MAGNESIUM
Similar Questions
Knowledge Check
- Question 1 - Select One
A particle moves along X-axis in such a way that its coordinate X varies with time t according to the equation x=(2−5t+6t2)m. The initial velocity of the particle is
A−5m/sB6m/sC−3m/sD3m/s - Question 2 - Select One
A particle moves along x-axis in such a way that its x-coordinate varies with time t according to the equation x=(8−4t+6t2) metre.
The velocity of the particle will vary with time according to the graph :-A B
B C
C D
D
- Question 3 - Select One
A particle moves along x-axis in such a way that its r-coordinate varies with time't according to the equation x= (8−4t+6t2) metre. The velocity of the particle will vary with time according to the graph
A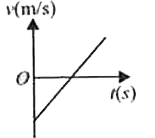 B
B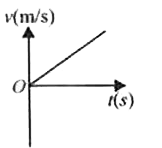 C
C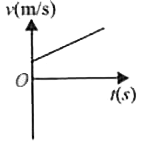 D
D
A particle is moving along x-axis. Its X-coordinate varies with time as, X=2t2+4t−6 Here, X is in meters and t in seconds. Find average velocity between the time interval t=0→t=2s.
View SolutionA particle moves along x axis in such a way that its coordinate x varies with time t according to the equation x=A0−A1t+A2t2. The initial velocity of the particle is.
View SolutionA particle moves along x− axis. It's velocity is a function of time according to relation V=(3t2−18t+24)m/s assume at t=0 particle is at origin.
Distance travelled by particle in 0 to 3 second time interval is :View SolutionA particle starts moving rectilinearly at time t = 0 such that its velocity v changes with time t according to the equation v=t2−t, where t is in seconds and v is in ms−1. The time interval for which the particle retrads (i.e., magnitude of velocity decreases)is
View SolutionA particle is moving with a velocity of v=(3+6t+9t2)ms. Find out
(a) the acceleration of the particle at t=3s.
(b) the displacement of the particle in the interval t=5s to t=8s.View Solution